Trang 64
Sau khi học xong bài này, em sẽ:
Vẽ được hình chiếu trục đo của vật thể đơn giản.
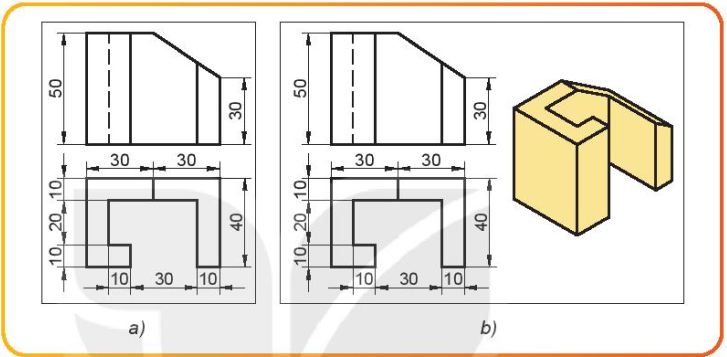
Hình 11.1
Hai hình trên cùng biểu diễn một vật thể. Hãy cho biết, cách biểu diễn nào giúp người xem dễ hình dung về hình dạng của vật thể hơn.
I - NỘI DUNG CỦA PHƯƠNG PHÁP HÌNH CHIẾU TRỤC ĐO
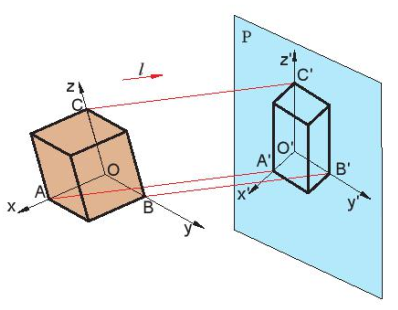
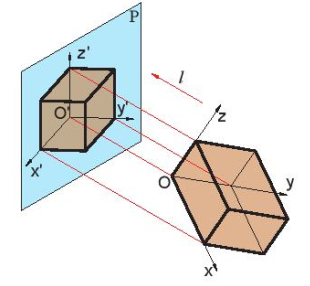
Hình 11.2. Xây dựng hình chiếu trục đo
Hình chiếu trục đo được xây dựng như sau (Hình 11.2):
- Gắn hệ trục toạ độ Oxyz vào vật thể, với các trục toạ độ đặt theo ba chiều dài, rộng và cao của vật thể. Chiếu vật thể cùng hệ trục toạ độ theo hướng l lên mặt phẳng hình chiếu P (l không song song P và không song song với mặt phẳng toạ độ nào). Kết quả trên mặt phẳng P nhận được một hình chiếu của vật thể và hệ toạ độ O'x'y'z'. Hình chiếu đó gọi là hình chiếu trục đo (HCTĐ) của vật thể.
- Các trục Ox, Oy và O'z gọi là các trục đo.
- Góc giữa các trục đo 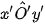 ,
,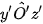 và
và 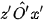 gọi là các góc trục đo.
gọi là các góc trục đo.
Trang 65
- Hệ số biến dạng là tỉ số độ dài hình chiếu một đoạn thẳng song song hoặc nằm trên trục toạ độ với độ dài thực tế của đoạn thẳng đó. Theo từng trục toạ độ, có các hệ số biến dạng như sau:
p = 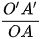 là hệ số biến dạng theo trục O'x'.
là hệ số biến dạng theo trục O'x'.
q = 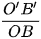 là hệ số biến dạng theo trục Oy.
là hệ số biến dạng theo trục Oy.
r = 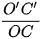 là hệ số biến dạng theo trục Oz'.
là hệ số biến dạng theo trục Oz'.
![]() Khám phá
Khám phá
a)
b)
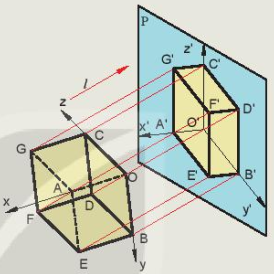
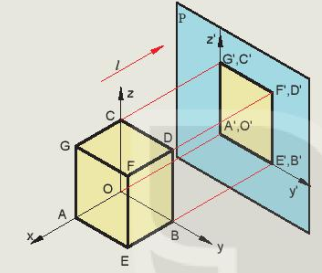
Hình 11.3. Vị trí hệ toạ độ ảnh hưởng đến hình chiếu của vật thể
Hãy quan sát Hình 11.3 và cho biết:
1. Các phép chiếu được sử dụng trên hình là những phép chiếu gì?
2. Vị trí tương đối giữa các trục toạ độ và mặt phẳng hình chiếu. Vị trí vật thể ở Hình 11.3b đã thay đổi như thế nào so với Hình 11.3a?
3. Nhận xét về hình chiếu thu được ở hai Hình 11.3a và Hình 11.3.
II – HÌNH CHIẾU TRỤC ĐO VUÔNG GÓC ĐỀU
Hình 11.4. Hình chiếu trục đo vuông góc đều
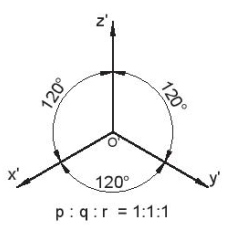
Hình 11.5. Góc trục đo và hệ số biến dạng
Trong hình chiếu trục đo vuông góc đều, phương chiếu I vuông góc với mặt phẳng hình chiếu P và các trục toạ độ Ox, Oy, Oz làm với mặt phẳng hình chiếu P các góc bằng nhau (Hình 11.4).
- Góc trục đo 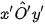 =
= 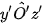 =
= 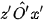 = 120°.
= 120°.
- Hệ số biến dạng p = q = r ≈ 0,82. Để thuận tiện cho việc dựng hình, quy ước lấy p = q = r = 1.
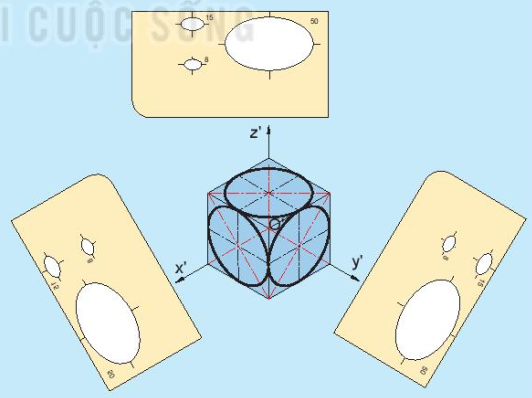
- Hình chiếu trục đo của hình tròn: hình chiếu trục đo vuông góc đều của những hình tròn nằm trên các mặt phẳng song song với các mặt phẳng toạ độ là các hình elip có phương của trục dài khác nhau (Hình 11.6).
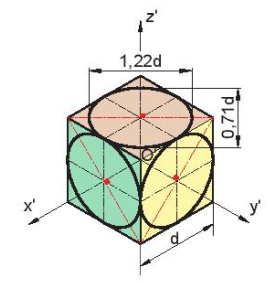
Hình 11.6. Các elip trong HCTĐ vuông góc đều
![]() Khám phá
Khám phá
Quan sát Hình 11.6 và cho biết:
1. Phương trục dài của elip khi hình tròn nằm trên mặt phẳng song song với mặt xOy, yOz và zOx có vị trí tương đối như thế nào so với các trục O'x', O'y', O'z'?
2. Kích thước của trục dài và trục ngắn của elip bằng bao nhiêu?
![]() Thông tin bổ sung
Thông tin bổ sung
1. Có thể dùng thước elip để vẽ hình chiếu trục đo của các đường tròn nằm trên mặt phẳng song song với các mặt toạ độ như sau (Hình 11.7):
- Bước 1. Xác định tâm elip.
- Bước 2. Vẽ các trục dài và trục ngắn của elip.
- Bước 3. Chọn elip có chỉ số bằng đường kính đường tròn, đặt thước sao cho hai trục của nó trùng với hai trục vẽ ở bước 2 và tô.
Hình 11.7. Cách đặt thước elip để tô
2. Cho phép dùng cách vẽ gần đúng hình elip bằng com pa. Các bước vẽ được trình bày trên Hình 11.8.
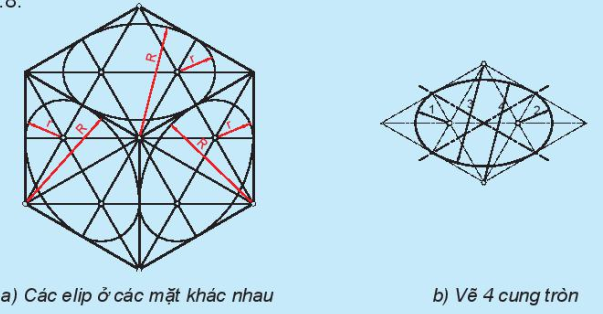
a) Các elip ở các mặt khác nhau
b) Vẽ 4 cung tròn
Hình 11.8. Cách vẽ gần đúng elip bằng com pa
III – HÌNH CHIẾU TRỤC ĐO XIÊN GÓC GÂN
Trong hình chiếu trục đo xiên góc cân, mặt phẳng toạ độ xOz song song với mặt phẳng hình chiếu P, I không vuông góc với P (Hình 11.9).
- Góc trục đo 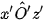 = 90°,
= 90°, 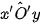 =
= 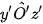 = 135°.
= 135°.
- Hệ số biến dạng p = r = 1, q = 0,5.
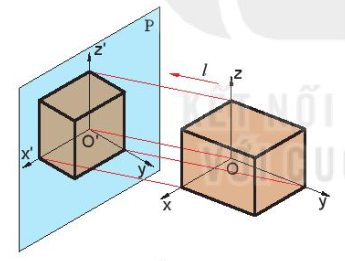
Hình 11.9. Hình chiếu trục đo xiên góc cân
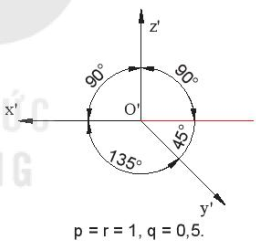
Hình 11.10. Góc trục đo và các hệ số biến dạng
Hình 11.11 là hình chiếu trục đo xiên góc cân của một hình lập phương có các hình tròn nội tiếp trong các mặt. Hình chiếu trục đo của hình tròn nằm trên mặt phẳng song song với mặt phẳng toạ độ xOz là hình tròn. Hình tròn nằm trên mặt phẳng song song với mặt toạ độ xOy hoặc yOz có hình chiếu trục đo là elip. Trục dài của elip bằng 1,06d, trục ngắn bằng 0,33d (d là đường kính của đường tròn). Trục dài của elip làm với trục nằm ngang hoặc trục thẳng đứng một góc 7°.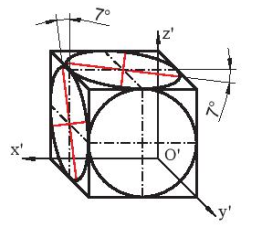
Hình 11.11. Các elip trong HCTĐ xiên góc cân
Trang 68
![]() Luyện tập
Luyện tập
Quan sát Hình 11.12 và cho biết:
1. Hình nào là hình chiếu trục đo vuông góc đều, hình nào là hình chiếu trục đo xiên góc cân?
2. Cặp hình nào là hình chiếu trục đo của cùng một vật thể?
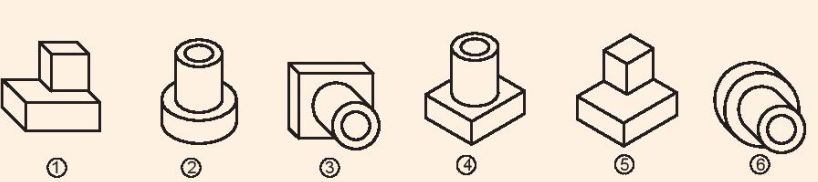
Hình 11.12. Hình chiếu trục đo vuông góc đều và xiên góc cân
IV – VẼ HÌNH CHIẾU TRỤC ĐO
1. Vẽ hình chiếu trục đo của một điểm
Một điểm A có hình chiếu đứng là 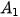 , hình chiếu bằng
, hình chiếu bằng 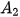 thì điểm A có các toạ độ
thì điểm A có các toạ độ 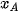 ,
, 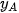 ,
, 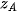 được đo như trên Hình 11.13a. Hình chiếu trục đo của điểm A là điểm A' có các toạ độ trục đo là
được đo như trên Hình 11.13a. Hình chiếu trục đo của điểm A là điểm A' có các toạ độ trục đo là 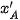 ;
; 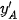 ,
, 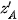 , với
, với 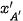 = p ×
= p × 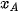 ,
, 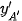 = q ×
= q × 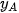 ,
, 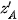 = r ×
= r × 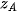 và được vẽ như Hình 11.13b.
và được vẽ như Hình 11.13b.
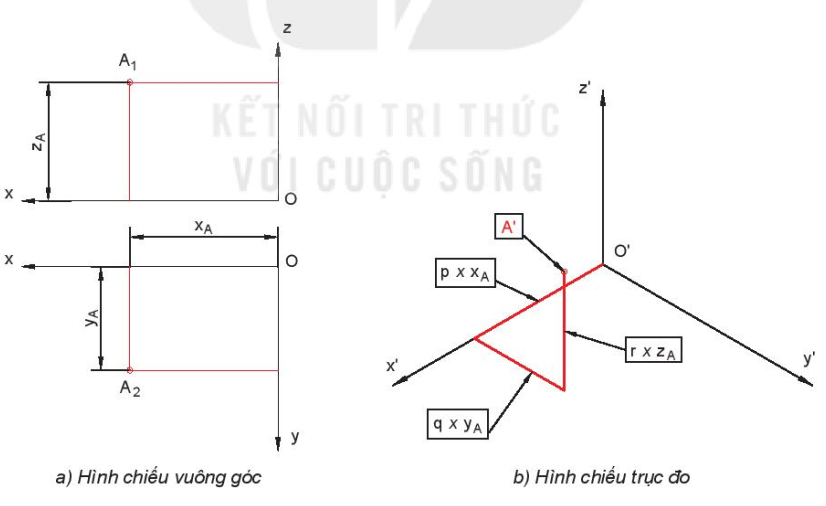
a) Hình chiếu vuông góc
b) Hình chiếu trục đo
Hình 11.13. Cách vẽ hình chiếu trục đo của một điểm
Trang 69
2. Vẽ hình chiếu trục đo của vật thể
Bước 1. Gắn hệ trục toạ độ Oxyz vào vật thể. Từ các hình chiếu vuông góc đã cho, phác hoạ hình dáng không gian của vật thể.
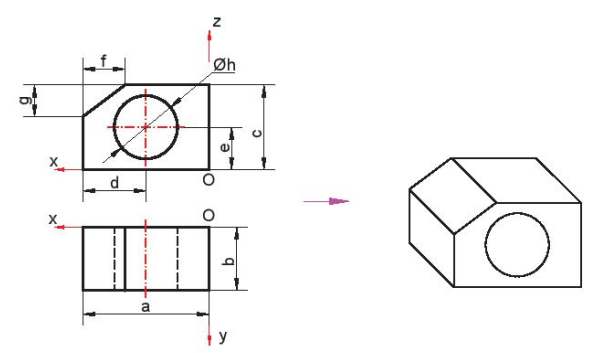
Hình 11.14. Gắn hệ trục và phác hoạ vật thể
Bước 2. Vẽ hình chiếu trục đo của hình hộp bao ngoài vật thể có kích thước: dài a rộng b và cao c đặt lên ba trục đo theo hệ số biến dạng của chúng.
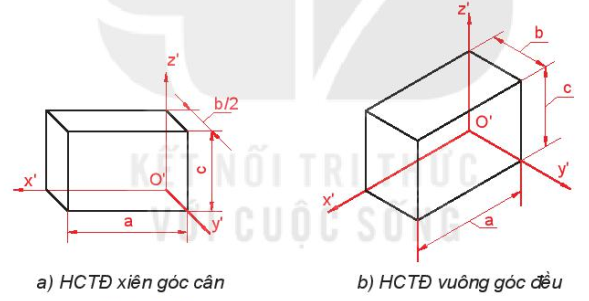
a) HCTĐ xiên góc cân
b) HCTĐ vuông góc đều
Hình 11.15. Vẽ hình hộp chữ nhật bao ngoài vật thể
Bước 3. Vẽ các thành phần của vật thể.
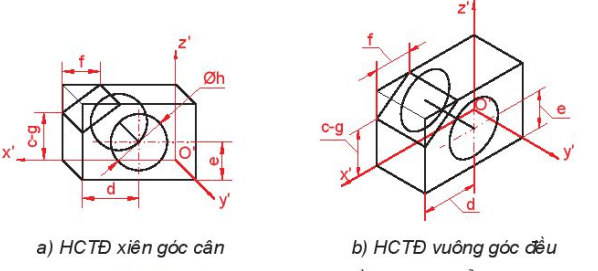
a) HCTĐ xiên góc cân
b) HCTĐ vuông góc đều
Hình 11.16. Vẽ các thành phần của vật thể
Trang 70
Bước 4. Tẩy các đường nét phụ, đường khuất, tô đậm các cạnh thấy.
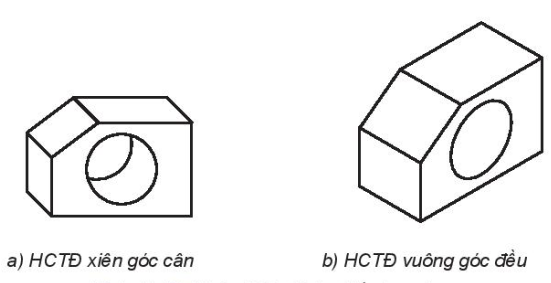
a) HCTĐ xiên góc cân
b) HCTĐ vuông góc đều
Hình 11.17. Hoàn thiện hình chiếu trục đo
![]() Thực hành
Thực hành
Cho hình chiếu đứng và hình chiếu bằng của Gối đỡ (Hình 11.18) và Đế (Hình 11.19). Hãy vẽ hình chiếu trục đo của một trong hai vật thể đó.
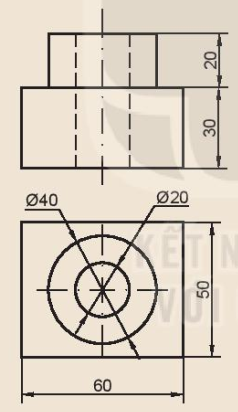
Hình 11.18. Gối đỡ
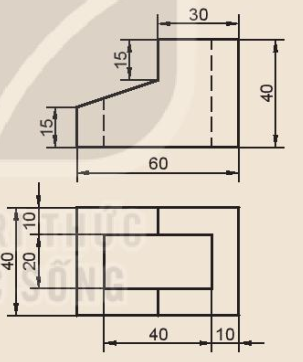
Hình 11.19. Đế
![]() Vận dụng
Vận dụng
Hãy vẽ hình chiếu trục đo của các đồ vật trong gia đình.

























