(Trang 56)
Ví dụ
Chứng minh rằng hình thang có hai cạnh đáy không bằng nhau, hai cạnh bên bằng nhau nhưng không song song là hình thang cân.
Giải
| GT | Hình thang ABCD; AB II CD; AB < CD; AD = BC; AD không song song BC. |
| KL | ABCD là hình thang cân. |

Hình 3.24
Qua điểm B kẻ đường thẳng song song với đường thẳng AD, cắt đường thẳng CD tại điểm E. Điểm E phải khác C vì nếu E trùng với C thì AD và BC song song, trái với giả thiết (H.3.24).
Hai tam giác EDA và ABE có: 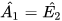 = E, (do AD // BE), AE là cạnh chung,
= E, (do AD // BE), AE là cạnh chung, 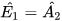 (do AB // DC).
(do AB // DC).
Vậy ΔEDA = ΔABE; suy ra AD = BE (hai cạnh tương ứng). Hơn nữa, theo giả thiết AD = BC nên BE = BC. Từ đó có ΔBEC cân tại B, suy ra 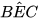 =
=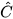 . Mặt khác,
. Mặt khác, 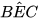 =
=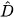 (do AD // BE) nên Ĉ =
(do AD // BE) nên Ĉ = 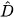 .
.
Vậy ABCD là hình thang cân.
BÀI TẬP
3.9. Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?

Hình 3.25
3.10. Cho hình thang cân ABCD (AB II CD) có AB = AD. Biết 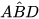 = 30°, tính số đo các góc của hình thang đó.
= 30°, tính số đo các góc của hình thang đó.
3.11. Tính số đo các góc của tứ giác ABCD trong Hình 3.26.
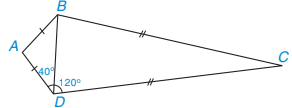
Hình 3.26
3.12. Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.
a) Chứng minh tứ giác APMR là hình thang cân.
b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.
c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?