(Trang 22)
Bài 5: PHÉP CHIA ĐA THỨC CHO ĐƠN THỨC
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| Đa thức A chia hết cho đa thức B |
|
Cho hai khối hộp chữ nhật: khối hộp thứ nhất có ba kích thước là x, 2x và 3y; khối hộp thứ hai có diện tích đáy là 2xy. Tình chiều cao (cạnh bên) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.
Trong bài toán này, thể tích của khối hộp thứ nhất là V=x.2x.3y=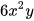
. Vì hai khối hộp có cùng thể tích nên đó cũng là thể tích của khối hộp thứ hai. Do đó, để tính chiều cao của khối hộp thứ hai, ta cần chia 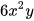cho 2xy.
Học xong bài này các em không những sẽ thực hiện được phép chia đó mà hơn nữa, còn biết cách chia một đa thức cho một đơn thức.
1. CHIA ĐƠN THỨC CHO ĐƠN THỨC
Cho hai đa thức A và B và B≠0 (tức là B khác đa thức 0). Tương tự đối với đa thức một biến, ta nói đa thức A chia hết cho đa thức B nếu có đa thức Q sao cho A=B.Q.
Khi đó ta viết A:B=Q, hoặc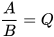 
.
Dưới đây, ta chỉ xét phép chia hết cho một đơn thức.
Chia một đơn thức cho một đơn thức
HĐ1 Hãy nhớ lại cách chia đơn thức cho đơn thức trong trường hợp chúng có cùng một biến và hoàn thành các yêu cầu sau:
a) Thực hiện phép chia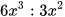 
b) Với a, b ∈ R và b≠0; m, n ∈ N, hãy cho biết:
- Khi nào thì
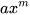chia hết cho 
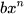. - Nhắc lại cách thực hiện phép chia 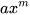cho .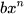
(Trang 23)
HĐ2 Với mỗi trường hợp sau, hãy đoán xem đơn thức A có chia hết cho đơn thức B không; nếu chia hết, hãy tìm thường của phép chia A cho B và giải thích cách làm:
a)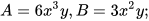 
b)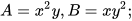 
| Hãy lần lượt chia: hệ số cho hệ số, lũy thừa của mỗi biến trong A cho lũy thừa của cùng biến đó trong B. |
Ta có kết luận sau đây:
a) Đơn thức A chia hết cho đơn thức B (B≠0) khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mữ của nó trong A.
b) Muốn chia đơn thức A cho đơn thức B (trường hợp chia hết), ta làm như sau:
- Chia hệ số của đơn thức A cho hệ số của đơn thức B;
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B;
- Nhân các kết quả tìm được với nhau.
Ví dụ 1:
Cho đơn thức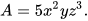 
a) Giải thích tại sao A không chia hết cho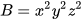 
;
b) Giải thích tại sao A chia hết cho C=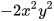
. Tìm thương của phép chưa A:C.
Giải
a) Ta thấy số mũ của y trong B là 2, lớn hơn số mũ của y trong A (là 1). Do đó, A không chia hết cho B.
b) A chia hết cho C vì số mũ của các biến x và z trong C cùng bằng 2, không lớn hơn số mũ của x (bằng 2) và z (bằng 3) trong A. Ta có:
.
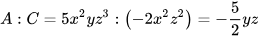Luyện tập 1:
Trong các phép chia sau đây, phép chia nào không là phép chia hết? Tại sao? Tìm phương của các phép chia còn lại:
a)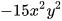 
chia cho 
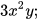b) 6xy chia cho 2yz c)
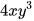chia cho 
.
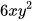Vận dụng 1:
Giải bài toán mở đầu.
(Trang 24)
2. CHIA ĐA THỨC CHO ĐƠN THỨC
Chia một đa thức cho một đơn thức
Dưới đây là quy tắc chia một đa thức cho một đơn thức trong trường hợp mọi hạng tử của đa thức đều chia hết cho đơn thức:
- Đa thức A chia hết cho đơn thưc B nếu mọi hạng tử của A đều chia hết cho B.
- Muốn chia đa thức A cho đơn thức B (trường hợp chia hết), ta chia từng hạng tử của A cho B rồi cộng các kết quả với nhau.
Ví dụ 2:
Thực hiện phép chia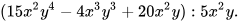 
Giải
=
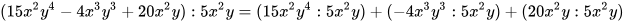
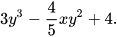
Luyện tập 2:
Làm tính chia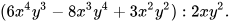 
Vận dụng 2
Tìm đa thức A sao cho A . (-3xy)=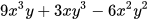
.
BÀI TẬP
1.30. a) Tìm đơn thức M, biết rằng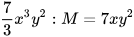 
.
b) Tìm đơn thức N sao cho N: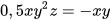 
.
1.31. Cho đa thức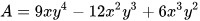 
. Với mỗi trường hợp sau đây, xét xem A có chia hết cho đơn thức B hay không? Thực hiện phép chia trong trường hợp A chia hết cho B.
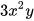a) B=
; b)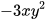 
.
1.32. Thực hiện phép chia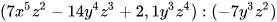 
.
