(Trang 29)
Chương II: HẰNG ĐẲNG THỨC ĐÁNG NHỚ VÀ ỨNG DỤNG
Ta có thể sử dụng nhiều tính chất đại số để tính toán nhanh hơn, chẳng hạn dùng hằng đẳng thức để tính nhanh giá trị của 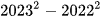 . Em có biết làm thế nào để tính nhanh biểu thức này không?
. Em có biết làm thế nào để tính nhanh biểu thức này không?
Bài 6: HIỆU HAI BÌNH PHƯƠNG. BÌNH PHƯƠNG CỦA MỘT TỔNG HAY MỘT HIỆU
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
|
|
Trong một trò chơi trí tuệ trên truyền hình dành cho học sinh, người dẫn chương trình yêu cầu các bạn học sinh cho biết kết quả phép tính 198 . 202. Ngay lập tức một bạn đã chỉ ra kết quả đúng. Bạn ấy tính như thế nào mà nhanh thế nhỉ?

(Trang 30)
1. HẰNG ĐẲNG THỨC
Nhân biết hằng đẳng thức
Ta có (a+1).b=a.b+b
Trong đẳng thức trên, khi thau a, b,... bởi bất kì giá trị số nào thì hai vế của đẳng thức luôn nhận giá trị bằng nhau, ta gọi là đẳng thức như vậy là hằng đẳng thức.
Tổng quát ta có
Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.
| Hằng đẳng thức còn gọi là đồng nhất thức. |

Ví dụ 1: Các đẳng thức thường gặp
a+b=b+a; a.b=b.a; a(b+c)=ab+ac
là những hằng đẳng thức.
Ví dụ 2: Đẳng thức nào sau đây là hằng đẳng thức?
a) 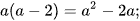 b)
b) 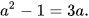
Giải
a) Đẳng thức 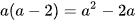 là hằng đẳng thức.
là hằng đẳng thức.
b) Đẳng thức 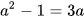 không phải là hằng đẳng thức (vì khi ta thay a=1 thì hai vế của đẳng thức không bằng nhau).
không phải là hằng đẳng thức (vì khi ta thay a=1 thì hai vế của đẳng thức không bằng nhau).
Luyện tập 1
Trong các đẳng thức sau, đẳng thức nào là hằng đẳng thức?
a) 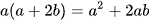 ; b) a+1=3a-1.
; b) a+1=3a-1.
2. HIỆU HAI BÌNH PHƯƠNG
Hiệu hai bình phương
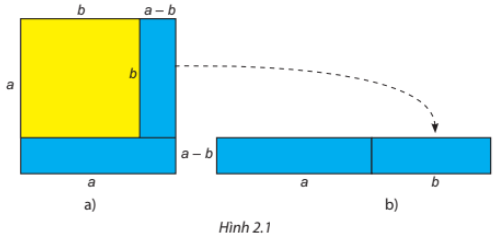
HĐ1 Quan sát hình 2.1.
(Trang 31)
a) Tính diện tích của phần hình màu xanh ở Hình 2.1a.
b) Tính diện tích hình chữ nhật màu xanh ở Hình 2.1a.
c) Có nhận xét gì về diện tích của hai hình ở câu a và câu b?
HĐ2 Với hai số a, b bất kì, thực hiện phép tính (a+b).(a-b).
Từ đó rút ra liên hệ giữa 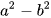 và (a+b)(a-b).
và (a+b)(a-b).
Với A, B là hai biểu thức tùy ý, ta cũng có:
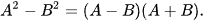
Ví dụ 3: a) Tính nhanh 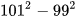 ; b) Viết
; b) Viết 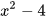 dưới dạng tích.
dưới dạng tích.
Giải
a) 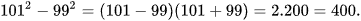
b)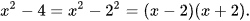
Luyện tập 2:
a) Tính nhanh 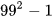 ; b) Viết
; b) Viết 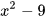 dưới dạng tích.
dưới dạng tích.
Vận dụng: Ở bài toán mở đầu, em hãy giải thích xem bạn đó tính nhanh như thế nào.
3. BÌNH PHƯƠNG CỦA MỘT TỔNG
Bình phương của một tổng
HĐ3 Với hai số a, b bất kì, thực hiện phép tính (a+b).(a+b).
Từ đó rút ra liên hệ giữa 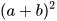 và
và 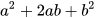 .
.
Với A, B là hai biểu thức tùy ý, ta có:
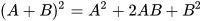 .
.
Ta nói khai triển 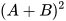 được biểu thức được biểu thức 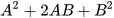 |

Ví dụ 4: a) Tính nhanh 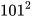 ; b) Khai triển
; b) Khai triển 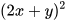 .
.
Giải
a) 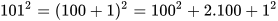
= 10 000+200+1=10 201.
b) 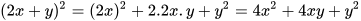 .
.
(Trang 32)
Vi dụ 5: Viết biểu thức 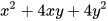 dưới dạng bình phương của một tổng.
dưới dạng bình phương của một tổng.
Giải
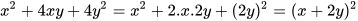 .
.
Luyện tập 3
- Khai triển
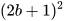 .
. - Viết biểu thức
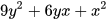 dưới dạng bình phương của một tổng.
dưới dạng bình phương của một tổng.
4. BÌNH PHƯƠNG CỦA MỘT HIỆU
Bình phương của một hiệu
HĐ4 Với hai số a, bi bất kì, viết a-b=a+(-b) và áp dụng hằng đẳng thức bình phương của một tổng để tính 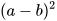 .
.
Với A, B là hai biểu thức tùy ý, ta có:
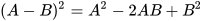 .
.
| Ta có thể tìm được hằng đẳng thưc bên bằng cách thực hiện nhân (A-B).(A-B). |

Ví dụ 6:
a) Tinh nhanh 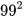 ; b) Khai triển
; b) Khai triển 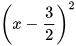 .
.
Giải
a) 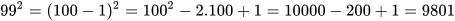 .
.
b) 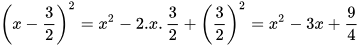 .
.
Luyện tập 4:
Khai triển 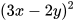 .
.
Vận dụng
Trong trò chơi “ Ai thông minh hơn học sinh lớp 8 ”, người dẫn chương trình yêu cầu các bạn học sinh cho biết kết quả của phép tính 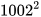 . Chỉ vài giây sau, Nam đã tính ra kết quả chính xác và giành được điểm. Em hãy giải thích xem Nam đã tính nhanh như thế nào.
. Chỉ vài giây sau, Nam đã tính ra kết quả chính xác và giành được điểm. Em hãy giải thích xem Nam đã tính nhanh như thế nào.
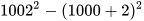 bạn nhé! bạn nhé! |

(Trang 33)
BÀI TẬP
2.1. Những đẳng thức nào sau đây là hằng đẳng thức?
a) x+2=3x+1; b) 2x(x+1)=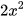 +2x;
+2x;
c) (a+b)a=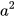 +ba; d) a-2=2a+1.
+ba; d) a-2=2a+1.
2.2. Thay ? bằng biểu thức thích hợp.
a) (x-3y)(x+3y)=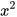 -? ;
-? ;
b) (2x-y)(2x+y)=4? - 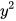 .
.
c) 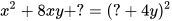 ;
;
d) 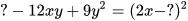 .
.
2.3. Tính nhanh:
a) 55.66; b) 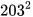 .
.
2.4. Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) 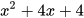 ; b)
; b)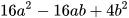 .
.
2.5. Rút gọn các biểu thức sau:
a)  ; b)
; b) 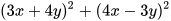 .
.
2.6. Chứng minh rằng với mọi số tự nhiên n, ta có:
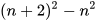 chia hết cho 4.
chia hết cho 4.