(Trang 64)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| Hình chữ nhật | • Mô tả khái niệm hình chữ nhật. • Giải thích tính chất hai đường chéo của hình chữ nhật. • Nhận biết dấu hiệu để một hình bình hành là hình chữ nhật. |
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
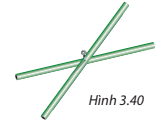
Hình 3.40
1 HÌNH CHỮ NHẬT
Khái niệm hình chữ nhật và tính chất
HĐ1 Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
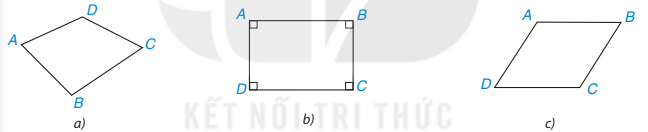
Hình 3.41
Hình chữ nhật là tứ giác có bốn góc vuông.
Chú ý. Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông và tứ giác đó là hình chữ nhật.
HĐ2 Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?
Ta có tính chất sau đây về đường chéo của hình chữ nhật:
| Hình chữ nhật có tất cả các tính chất của hình bình hành và của hình thang cân.
|
Định lí 1
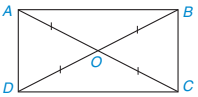
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường (H.3.42).
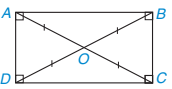
Hình 3.42
Nhận xét. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
(Trang 65)
Ví dụ 1 Cho hình chữ nhật ABCD, hai đường chéo AC và BD cắt nhau tại O. Chứng minh △OAB = △ODC.
Giải (H.3.43)
Vì ABCD là hình chữ nhật nên
.
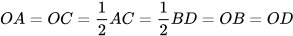Hai tam giác OAB và ODC có: OA=OD, OB = OC, AB = CD. Vậy △OAB = △ODC (c.c.c).
Hình 3.43
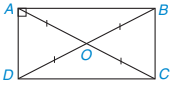
Luyện tập 1 Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H.3.44). Chứng minh rằng H là trung điểm của DC.
Hình 3.44
2 DẤU HIỆU NHẬN BIẾT
Dấu hiệu nhận biết hình chữ nhật
HĐ3 Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?
Ta cũng chứng minh được hình bình hành ABCD có hai đường chéo AC và BD bằng nhau là hình chữ nhật.
Định lí 2
a) Hình bình hành có một góc vuông là hình chữ nhật.
b) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
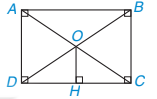
Ví dụ 2 Chứng minh rằng tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường thì tứ giác đó là hình chữ nhật.
Hình 3.45
Giải (H.3.45)
| GT | ABCD là tứ giác; O là giao điểm của AC và BD, AC = BD, OA = OC, OB = OD |
| KL | ABCD là hình chữ nhật. |
Theo giả thiết, O là trung điểm của cả AC và BD nên ta có ABCD là hình bình hành.
Hơn nữa, AC = BD nên theo Định lí 2, hình bình hành ABCD là hình chữ nhật.
(Trang 66)
Luyện tập 2 Cho tứ giác ABCD có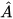 
= 90°, hai đường chéo cắt nhau tại trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?
Nhận xét. Nếu tam giác có một đường trung tuyến bằng nửa cạnh tương ứng thì tam giác đó là tam giác vuông.
Vận dụng. Hãy trả lời các câu hỏi trong tình huống mở đầu.
BÀI TẬP
3.25. Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.
3.26. Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Giải thích kết quả.
3.27. Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.
3.28. Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
