Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án đã cho để được khẳng định đúng.
Câu 80 trang 64 SGK
Hàm số ![]()
(A) Đồng biến trên khoảng (-2; 3);
(B) Nghịch biến trên khoảng (-2; 3);
(C) Nghịch biến trên khoảng (-∞; -2);
(D) Đồng biến trên khoảng (-; +∞).
Lời giải:
f′(x) = x2 − x − 6
f′(x) = 0 ⇔ x = −2 hoặc x = 3
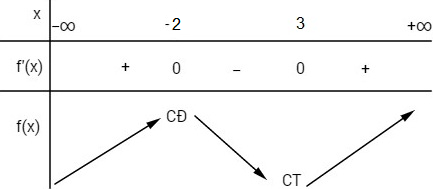
Từ bảng biến thiên ta thấy hàm số nghịch biến trên khoảng (−2; 3).
Chọn (B).
Câu 81 trang 64 SGK
Hàm số f(x) = 6x5 − 15x4 + 10x3 − 22
(A) Nghịch biến trên R;
(B) Đồng biến trên khoảng (−∞; 0) và nghịch biến trên khoảng (0; +∞);
(C) Đồng biến trên khoảng R;
(D) Nghịch biến trên khoảng (0; 1).
Lời giải:
f′ (x) = 30x4 − 60x3 + 30x2
= 30x2(x2 − 2x + 1)
= 30x2(x − 1)2 ≥ 0
f′(x) = 0 ⇔ x = 0 hoặc x = 1
Hàm số đồng biến trên R.
Chọn (C).
Câu 82 trang 64 SGK
Hàm số y = sinx − x
(A) Đồng biến trên R;
(B) Đồng biến trên khoảng (−∞; 0);
(C) Nghịch biến trên khoảng (−∞; 0) và đồng biến trên khoảng (0; +∞);
(D) Nghịch biến trên R.
Lời giải:
y′ = cosx − 1 ≤ 0 ∀x ∈ R.
Dấu bằng xảy ra khi và chỉ khi x = 2kπ
Hàm số nghịch biến trên R.
Chọn (D).
Câu 83 trang 64 SGK
Hàm số f(x) = x3 − 3x2 − 9x + 11
(A) Nhận điểm x = -1 làm điểm cực tiểu;
(B) Nhận điểm x = 3 làm điểm cực đại;
(C) Nhận điểm x = 1 làm điểm cực đại;
(D) Nhận điểm x = 3 làm điểm cực tiểu.
Lời giải:
f′ (x) = 3x2 − 6x − 9
f′ (x) = 0 ⇔ x = −1 hoặc x = 3
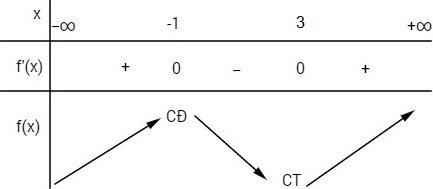
Hàm số đạt cực tiểu tại điểm x = 3.
Chọn (D).
Câu 84 trang 64 SGK
Hàm số y = x4 − 4x3 − 5
(A) Nhận điểm x = 3 làm điểm cực tiểu;
(B) Nhận điểm x = 0 làm điểm cực đại;
(C) Nhận điểm x = 3 làm điểm cực đại;
(D) Nhận điểm x = 0 làm điểm cực tiểu.
Lời giải:
y′ = 4x3 − 12x2 = 4x2(x − 3)
y′ = 0 ⇔ x = 0 hoặc x = 3.
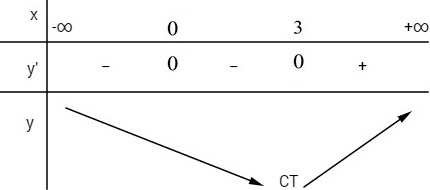
Hàm số đạt cực tiểu tại điểm x = 3.
Chọn (A).
Câu 85 trang 64 SGK
Số điểm cực trị của hàm số y = x4 − 2x2 − 3 là
(A) 0; (B) 1;
(C) 3; (D) 2.
Lời giải:
y′ = 4x3 − 4x = 4x(x2 − 1)
y′ = 0 ⇔ x = 0 hoặc x = 1 hoặc x = −1
Phương trình y′ = 0 có ba nghiệm phân biệt và y′ đổi dấu qua 3 nghiệm đó.
Hàm số có 3 điểm cực trị.
Chọn (C).
Câu 86 trang 64 SGK
Số điểm cực trị của hàm số ![]() là
là
(A) 0; (B) 2; (C) 1; (D) 3.
Lời giải:
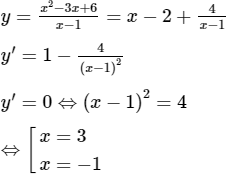
Phương trình y′ = 0 có hai nghiệm phân biệt và y′ đổi dấu qua 2 nghiệm đó.
Hàm số có 2 cực trị.
Chọn (B).
Câu 87 trang 64 SGK
Hàm số f có đạo hàm là f′(x) = x2(x + 1)2(2x − 1).
Số điểm cực trị của hàm số là
(A) 1; (B) 2;
(C) 0; (D) 3.
Lời giải:
Vì x2(x + 1)2 ≥ 0 ∀x ∈ R nên f’(x) chỉ đổi dấu khi x qua 1/2.
Hàm số có 1 điểm cực trị.
Cách khác:
Ta có:
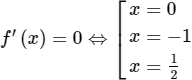
Qua điểm x = 0; x= -1 thì f’(x) không đổi dấu nên hai điểm này không là cực trị của hàm số.
Qua điểm x = 1/2 thì f’(x) đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại x = 1/2.
Vậy hàm số có 1 điểm cực trị.
Chọn (A).
Câu 88 trang 64 SGK
Hàm số y = x − sin2x + 3
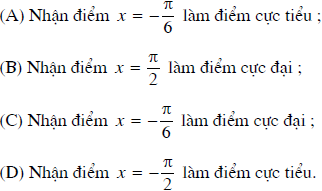
Lời giải:
y′ = 1 − 2cos2x;
y′′= 4sin2x.
Ta có: y′(−π/6) = 0 và y′′(−π/6) < 0
Hàm số nhận điểm x = −π/6 làm điểm cực đại.
Ngoài ra tại các điểm ±π/2 thì y′(±π/2) ≠ 0 nên không là điểm cực trị.
Cách khác:
f'(x) = 1 − 2cos2x, f' (-π/6) = 0 và đổi dấu từ dương sang âm tại điểm x = -π/6.
Chọn (C).
Câu 89 trang 64 SGK
Giá trị lớn nhất của hàm số ![]() là:
là:
(A) -3; (B) 1
(C) -1 (D) 0
Lời giải:
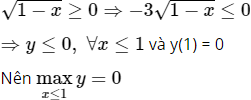
Chọn (D).
Câu 90 trang 64 SGK
Giá trị nhỏ nhất của hàm số y = 3sinx − 4cosx là:
(A) 3; (B) -5; (C) -4; (D) -3.
Lời giải:
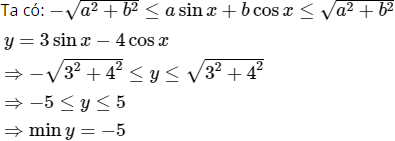
Cách khác:
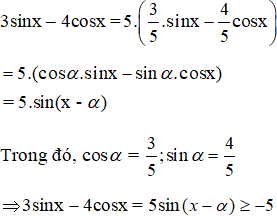
Chọn (B).
Câu 91 trang 64 SGK
Giá trị lớn nhất của hàm số
f(x) = 2x3 + 3x2 − 12x + 2 trên đoạn [−1; 2] là:
(A) 6; (B) 10;
(C) 15; (D) 11.
Lời giải:
f′(x) = 6x2 + 6x − 12
f′(x) = 0 ⇔ x = 1 ∈ [−1; 2] hoặc x = −2 ∉[−1; 2]
f(−1) = 15; f(1) = −5; f(2) = 6.
Vậy ![]()
Chọn (C).
Câu 92 trang 64 SGK
Giá trị lớn nhất của hàm số ![]() là:
là:
(A) 2; (B) √2
(C) 0; (D) 3.
Lời giải:
TXĐ: D = [−3; 1]
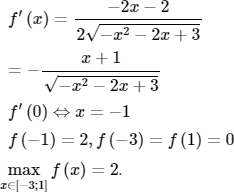
Cách khác:
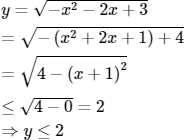
Chọn (A).
Câu 93 trang 64 SGK
Gọi (C) là đồ thị của hàm số ![]()
(A) Đường thẳng x = -1 là tiệm cận đứng của (C).
(B) Đường thẳng x = 2x − 1 là tiệm cận đứng của (C).
(C) Đường thẳng x = x + 1 là tiệm cận đứng của (C).
(D) Đường thẳng x = x − 2 là tiệm cận đứng của (C).
Lời giải:
TXĐ: x = −1/2
Lại có: ![]()
Tiệm cận xiên : y = x − 2.
Chọn (D).
Câu 94 trang 64 SGK
Gọi (C) là đồ thị của hàm số ![]()
(A) Đường thẳng x = 1 là tiệm cận đứng của đồ thị (C).
(B) Đường thẳng x = −1/2 là tiệm cận đứng của đồ thị (C).
(C) Đường thẳng y = 1 là tiệm cận ngang của đồ thị (C).
(D) Đường thẳng x = -x +1 là tiệm cận xiên của đồ thị (C).
Lời giải:
3 + 5x − 2x2 = 0 ⇔ x = −1/2 hoặc x = 3
Ta thấy x = −1/2 và x = 3 không là nghiệm của tử nên các đường thẳng x = −1/2 và x = 3 đều là TCĐ của đồ thị hàm số.
Chọn (B).
Câu 95 trang 64 SGK
Gọi (C) là đồ thị của hàm số ![]()
(A) Đường thẳng x = 2 là tiệm cận đứng của (C).
(B) Đường thẳng y = x − 1 là tiệm cận xiên của (C).
(C) Đường thẳng y = −1/5 là tiệm cận ngang của (C).
(D) Đường thẳng y = −1/2 là tiệm cận ngang của (C).
Lời giải:
limx→±∞ y = −1/5
Tiệm cận ngang y = −1/5
Chọn (C).
Câu 96 trang 64 SGK
Đồ thị của hàm số ![]()
(A) cắt đường thẳng y = 1 tại hai điểm;
(B) cắt đường thẳng y = 4 tại hai điểm;
(C) Tiếp xúc với đường thẳng y = 0;
(D) Không cắt đường thẳng y = -2.
Lời giải:
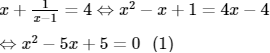
(1) có hai nghiệm phân biệt nên đồ thị cắt đường thẳng y = 4 tại hai điểm phân biệt.
Chọn (B).
Câu 97 trang 64 SGK
Xét phương trình x3 + 3x2 = m
(A) Với m = 5, phương trình đã có ba nghiệm;
(B) Với m = -1, phương trình có hai nghiệm;
(C) Với m = 4, phương trình đã có ba nghiệm phân biệt;
(D) Với m = 2, phương trình đã có ba nghiệm phân biệt.
Lời giải:
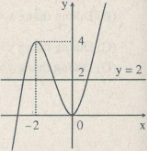
Vẽ đồ thị hàm số y = x3 + 3x2
y′ = 3x2 + 6x;
y′ = 0 ⇔ x = −2; y(−2) = 4 hoặc x = 0; y(0) = 0
m = 2: Phương trình có 3 nghiệm phân biệt.
Chọn (D).
Câu 98 trang 64 SGK
Đồ thị hàm số ![]()
(A) Nhận điểm (−1/2; 1/2) làm tâm đối xứng.
(B) Nhận điểm (−1/2; 2) làm tâm đối xứng.
(C) Không có tâm đối xứng.
(D) Nhận điểm (1/2; 1/2) làm tâm đối xứng.
Lời giải:
Tiệm cận đứng: x = −1/2;
Tiệm cận ngang: y = 1/2.
Giao điểm hai tiệm cận I(−1/2; 1/2) là tâm đối xứng của đồ thị hàm số.
Chọn (A).
Câu 99 trang 64 SGK
Số giao điểm của hai đường cong y = x3 − x2 − 2x + 3 và y = x2 − x + 1 là:
(A) 0; (B) 1; (C) 3; (D) 2.
Lời giải:
Hoành độ giao điểm của hai đường cong là nghiệm phương trình:
x3 − x2 − 2x + 3 = x2 − x + 1
⇔ x3 − 2x2 − x + 2 = 0
⇔ (x − 1)(x2 − x − 2) = 0
⇔ (x − 1)(x + 1)(x − 2) = 0
⇔ x = ±1 hoặc x = 2
Chọn (C).
Câu 100 trang 64 SGK
Các đồ thị của hai hàm số y = 3 − 1x và y = 4x2 tiếp xúc với nhau tại M có hoành độ là:
(A) x = -1; (B) x = 1; (C) x = 2; (D) x = 1/2.
Lời giải:
Ta có:
f(x) = 3 − 1/x ⇒ f′(x) = 1/x2
g(x) = 4x2 ⇒ g′(x) = 8x
Đồ thị hàm số y = f(x) tiếp xúc với đồ thị hàm số y = g(x)
⇔ hoành độ tiếp điểm là nghiệm của hệ 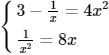
Ta có:
1/x2 = 8x ⇔ 1 = 8x3 ⇔ x3 = 1/8 ⇔ x = 1/2
Thay x = 1/2 vào phương trình đầu ta được:
![]() nên hệ trên có nghiệm x = 1/2.
nên hệ trên có nghiệm x = 1/2.
Chọn (D).

























