4(Trang 47)
| Thuật ngữ
| Kiến thức, kĩ năng
|
| Sao chổi Borisov (2I/Borisov) chuyển động theo quỹ đạo hypebol với tâm sai khoảng 3,3567 (theo:minor.planetcenter.net), chỉ đi vào hệ Mặt Trời một lần, không quay lại (H.3.11). Chỉ với thông tin tâm sai, máy tính đã có thể vẽ được hình ảnh thu nhỏ của hypebol quỹ đạo. Vậy tâm sai của hypebol là gì? Ta sẽ cùng tìm hiểu trong bài học này. |
Hình 3.11 Sao chổi Borisov được phát hiện vào ngày 30/8/2019 bởi nhà thiên văn học nghiệp dư Gennady Borisov. |
1. HÌNH DẠNG CỦA HYPEBOL
> HĐ1. Trong mặt phằng toạ độ, cho hypebol có phương trình chính tắc 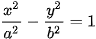 .
.
a) Hãy giải thích vì sao nếu điểm M(x0, y0) thuộc hypebol thì các điềm có toạ độ (x0, -y0), (-x0, y0), (-x0, -y0) cũng thuộc hypebol (H.3.12).
b) Tìm toạ độ các giao điềm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?
c) Với điểm M(x0, y0) thuộc hypebol, hãy so sánh 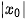 với a.
với a.
(Trang 48)
| Cho hypebol có phương trình chính tắc
|
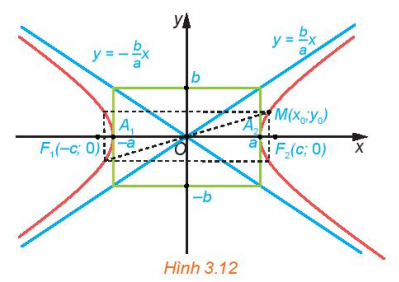
Chú ý. Trong hypebol nói trên, nhánh chứa đỉnh A2(a; 0) là nhánh gồm các điềm M thoả mãn MF1 - MF2= 2a, nhánh chứa đỉnh A1(-a; 0) là nhánh gồm các điềm M thoả mãn MF1 - MF2= 2a (với F1(-c; 0), F2(c; 0) là các tiêu điểm,  ).
).
>Ví dụ 1. Cho hypebol 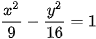
a) Tìm độ dài các trục, toạ độ các đỉnh.
b) Tìm các đường tiệm cận.
Giải
Từ phương trình của hypebol, ta có a2 = 9, b2 = 16, nghĩa là a = 3, b = 4.
a) Hypebol có độ dài trục thực là 2a = 6, độ dài trục ảo là 2b = 8, và hai đỉnh là A1(-3; 0), A2(3; 0).
Chú ý. Hai đường tiệm cận không cắt hypebol. Hơn nữa khi một điểm thay đồi trên hypebol thì càng xa gốc toạ độ, khoảng cách từ nó tới một trong hai đường tiệm cận càng gần bằng 0 (điều này giải thích cho việc dùng từ “tiệm cận").
>Luyện tập 1. Cho hypebol 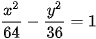 .
.
a) Tìm tiêu cự và độ dài các trục.
b) Tìm các đỉnh và các đường tiệm cận.
(Trang 49)
2. BÁN KÍNH QUA TIÊU, TÂM SAI VÀ ĐƯỜNG CHUẨN
>HĐ2. Cho điểm M(x0, y0) thuộc hypebol có hai tiêu điểm F1(-c; 0), F2(c; 0), độ dài trục thực bằng 2a.
a) Tính 
b) Giả sử M(x0, y0) thuộc nhánh chứa đỉnh A2(a; 0), tức là, MF1 - MF2= 2a. Tính MF1 + MF2, MF1, MF2.
b) Giả sử M(x0, y0) thuộc nhánh chứa đỉnh A1(-a; 0), tức là, MF1 - MF2= 2a. Tính MF1 + MF2, MF1, MF2.
| Cho hypebol có phương trình chính tắc
Các đoạn thằng MF1, MF2 được gọi là bán kính qua tiêu của điểm M. |
? Hiệu độ dài hai bán kính qua tiêu của một điềm thuộc hypebol có mối quan hệ gì với độ dài trục thực?
Chú ý. Mặc dù công thức độ dài bán kính qua tiêu nói trên có chứa dấu giá trị tuyệt đối, nhưng từ đó, em cũng có thề dễ dàng suy luận ngược trở lại công thức bán kính qua tiêu ứng với từng nhánh hypebol mà em đã đạt được trong HĐ2:
Nếu M(x; y) thuộc nhánh chứa đỉnh A2(a; 0)
thì 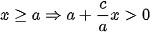 nên
nên 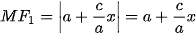 và
và 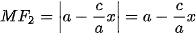 (để ý rằng c> a).
(để ý rằng c> a).
Nếu M(x; y) thuộc nhánh chứa đỉnh A1(-a; 0)
thì 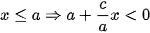 (để y rằng c > a) nên
(để y rằng c > a) nên 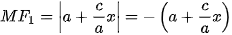 và
và 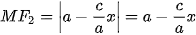 .
.
>Ví dụ 2. Cho hypebol 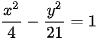 . Tính độ dài hai bán kính qua tiêu của một điềm M thuộc hypebol và có hoành độ bằng –10.
. Tính độ dài hai bán kính qua tiêu của một điềm M thuộc hypebol và có hoành độ bằng –10.
Giải
Ta có a2 = 4; b2= 21. Suy ra a = 2, b= 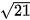 , và
, và 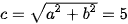 . Do đó, hypebol có hai tiêu điểm là F1(-5; 0), F2(5; 0). Điểm M thuộc hypebol và có hoành độ x0 = -10 nên
. Do đó, hypebol có hai tiêu điểm là F1(-5; 0), F2(5; 0). Điểm M thuộc hypebol và có hoành độ x0 = -10 nên
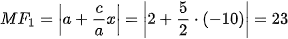 và
và 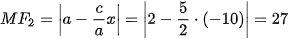 .
.
(Trang 50)
>Luyện tập 2. Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng 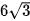 . Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
. Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
>Ví dụ 3. Cho hypebol có phương trình chính tắc 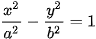 . Tìm điềm Mtrên hypebol đề khoảng cách từ M đến tiêu điểm F2(c; 0) nhỏ nhất (H.3.13).
. Tìm điềm Mtrên hypebol đề khoảng cách từ M đến tiêu điểm F2(c; 0) nhỏ nhất (H.3.13).
Giải
Với mỗi điểm M(x0, y0) ) thuộc hypebol, ta có bán kính qua tiêu của M ứng với tiêu điểm F2 là 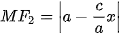 .
.
- Nếu M(x0, y0) thuộc nhánh chứa đỉnh A2(a; 0) thì x0 ≥ a nên 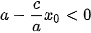 (đề ý rằng c > a). Do đó, (đề ý rằng c > a). Do đó, 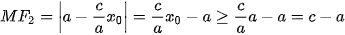 | 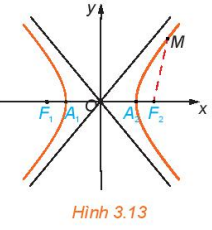 |
Dấu đằng thức xảy ra khi x0 = a, tức là, khi M(x0, y0) trùng đỉnh A2(a; 0).
- Nếu M(x0, y0) thuộc nhánh chứa đỉnh A1(-a; 0) thì x0 ≤ -a nên 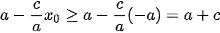 . Suy ra
. Suy ra
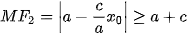
Vậy điểm M(x0, y0) thuộc hypebol có khoảng cách tới tiêu điểm F2(c; 0) nhỏ nhất khi M trùng đỉnh A2(a; 0), và khi đó, khoảng cách bằng c- a.
Chú ý. Tương tự Ví dụ 3, khoảng cách từ điểm M thuộc hypebol đến tiêu điềm F1(-c; 0) nhỏ nhất khi M trùng đỉnh A1(-a; 0) và khi đó, khoảng cách bằng c- a.
>Luyện tập 3. Cho hypebol 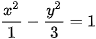 với hai tiêu điểm F1(-2; 0), F2(2; 0). Điểm M nào thuộc hypebol mà có độ dài bán kính qua tiêu MF2 nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm.
với hai tiêu điểm F1(-2; 0), F2(2; 0). Điểm M nào thuộc hypebol mà có độ dài bán kính qua tiêu MF2 nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm.
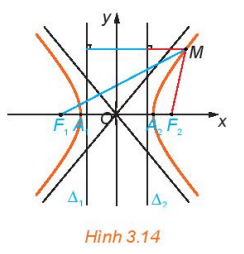
>HĐ3. Cho hypebol có phương trình chính tắc 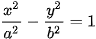 với các tiêu điểm F1(-c; 0), F2(c; 0). Xét các đường thẳng
với các tiêu điểm F1(-c; 0), F2(c; 0). Xét các đường thẳng 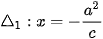 và
và 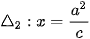 (H.3.14). Với điểm M(x; y) thuộc hypebol, tính các tỉ số
(H.3.14). Với điểm M(x; y) thuộc hypebol, tính các tỉ số 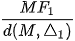 và
và 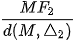 theo a và c.
theo a và c.

Bán kính qua tiêu có độ dài nhỏ nhất bằng nửa hiệu của độ dài tiêu cự và trục thực.
(Trang 51)
|  |
Chú ý
- Tâm sai e của hypebol là một số lớn hơn 1.
- Độ dài các bán kính qua tiêu của điềm M(x; y) thuộc hypebol còn được viết dưới dạng
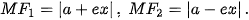
>Ví dụ 4. Tìm tâm sai và các đường chuẩn của hypebol 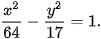
Giải
Ta có a2= 64, b2= 17. Suy ra a = 8, b=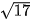 và
và 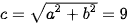 . Do đó, hypebol có tâm sai là
. Do đó, hypebol có tâm sai là 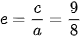 và các đường chuẩn là
và các đường chuẩn là 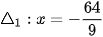 (ứng với tiêu điểm F1(-9; 0)) và
(ứng với tiêu điểm F1(-9; 0)) và 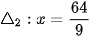 (ứng với tiêu điểm F2(9; О)).
(ứng với tiêu điểm F2(9; О)).
>Ví dụ 5. Trong mặt phẳng toạ độ Oxy, hypebol (H) có phương trình chính tắc, đi qua điểm A(4; 0) và có tâm sai e = 3. Tim phương trình của (H).
Giải. Phương trình chính tắc của hypebol có dạng
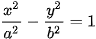
Vì hypebol đi qua điềm A(4; 0) nên ta có
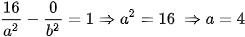
Theo công thức tính tâm sai ta có
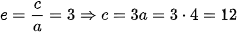
(Trang 51)
Do đó b2= c2- a2= 122- 42= 128.
Vậy phương trình chính tắc của hypebol là 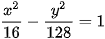
>Luyện tập 4. Trong mặt phẳng toạ độ Oxy, hypebol (H) có phương trình chính tắc, có tâm sai e = 2 và một đường chuần là x = 8. Lập phương trình chính tắc của (H).
>Ví dụ 6. Giải thích vì sao ta có thể dùng hình vẽ một hypebol (H) bắt kì với tâm sai e = 3,3567 như là một hình ảnh thu nhỏ của hypebol chứa quỹ đạo của sao chồi Borisov mà ta đã gặp ở đầu bài học.
Giải
Giả sử hình (H) có độ dài trục thực bằng 2a mét, tiêu cự bằng 2c mét, và hypebol chứa quỹ đạo của sao chỗi Borisov có độ dài trục thực bằng 2a' mét, tiêu cự bằng 2c' mét. Ta có, 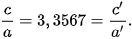 Vậy, nếu đặt
Vậy, nếu đặt 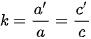 thì (H) là bản vẽ thu nhỏ của hypebol chứa sao chổi Borisov, với tỉ lệ 1: k.
thì (H) là bản vẽ thu nhỏ của hypebol chứa sao chổi Borisov, với tỉ lệ 1: k.
Nhận xét. Qua Ví dụ 6 ta thấy, tâm sai của hypebol (tương tự của elip) quyết định hình dạng của hypebol (elip).
| >Vận dụng. Một sao chổi đi qua hệ Mặt Trời theo quỹ đạo là một nhánh hypebol nhận tâm Mặt Trời là một tiêu điềm, khoảng cách gần nhất từ sao chổi này đến tâm Mặt Trời là 3·108 km và tâm sai của quỹ đạo hypebol là 3,6 (H.3.15). Hãy lập phương trình chính tắc của hypebol chứa quỹ đạo, với 1 đơn vị đo trên mặt phằng toạ độ ứng với 108 km trên thực tế. | 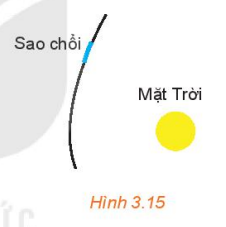 |
BÀI TẬP
3.7. Trong mặt phẳng toạ độ, cho hypebol có phương trình chính tắc 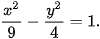 Xác định toạ độ các đỉnh, độ dài các trục, tâm sai và phương trình các đường chuẩn của hypebol.
Xác định toạ độ các đỉnh, độ dài các trục, tâm sai và phương trình các đường chuẩn của hypebol.
3.8. Trong mặt phẳng toa độ, cho hypebol có phương trình chính tắc 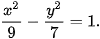 Tính bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 12.
Tính bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 12.
3.9. Trong mặt phằng toạ độ, hypebol (H) có phương trình chính tắc. Lập phương trình chính tắc của (H) trong mỗi trường hợp sau:
a) (H) có nửa trục thực bằng 4, tiêu cự bằng 10;
b) (H) có tiêu cự bằng 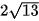 , một đường tiệm cận là
, một đường tiệm cận là 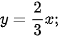
c) (H) có tâm sai e = 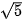 , và đi qua điểm
, và đi qua điểm 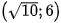
3.10. Một hypebol mà độ dài trục thực bằng độ dài trục ảo được gọi là hypebol vuông. Tìm tâm sai và phương trình hai đường tiệm cận của hypebol vuông.
3.11. Chứng minh rằng tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.
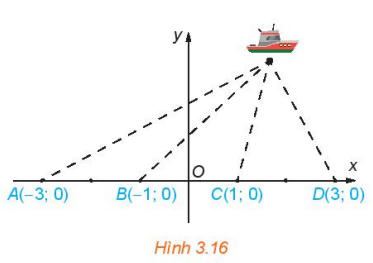
3.12. Bốn trạm phát tín hiệu vô tuyến có vị trí A, B, C. D theo thứ tự đó thẳng hàng và cách đều với khoảng cách 200 km (H.3.16). Tại một thời điểm, bốn trạm cùng phát tín hiệu với vận tốc 292 000 km/s. Một tàu thuỷ nhận được tín hiệu từ trạm C trước 0,0005 s so với tín hiệu từ trạm B và nhận được tín hiệu từ trạm D sớm 0,001 s so với tín hiệu từ trạm A.
a) Tính hiệu các khoảng cách từ tàu đến các trạm B, C.
b) Tính hiệu các khoảng cách từ tàu đến các trạm A, D.
c) Chọn hệ trục toạ độ Oxy như trong Hình 3.16 (1 đơn vị trên mặt phẳng toạ độ ứng với 100 km trên thực tế). Hãy lập phương trình chính tắc của hai hypebol đi qua vị trí M của tàu. Từ đó, tính toạ độ của M (làm tròn kết quả đến chữ số thập phân thứ năm).
d) Tính các khoảng cách từ tàu đến các trạm B, C (đáp số được làm tròn đến hàng đơn vị, tính theo đơn vị km).

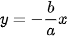 và
và 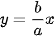 .
.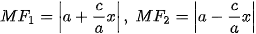
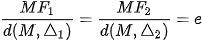 không đổi, trong đó
không đổi, trong đó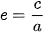 được gọi là tâm sai của hypebol.
được gọi là tâm sai của hypebol.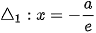 và
và 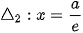 được gọi là các đường chuẩn tương ứng với F1(-c; 0) và F2(c; 0) của hypebol.
được gọi là các đường chuẩn tương ứng với F1(-c; 0) và F2(c; 0) của hypebol.
























