Trang 66
| THUẬT NGỮ • Góc giữa hai vectơ • Tích vô hướng của hai vectơ | KIẾN THỨC, KĨ NĂNG • Tính góc, tích vô hướng của hai vectơ trong những trường hợp cụ thể. • Công thức toạ độ của tích vô hướng, tính chất của tích vô hướng. • Liên hệ khái niệm tích vô hướng với khái niệm công trong Vật lí. |
Toán học cung cấp ngôn ngữ và công cụ cho nhiều ngành khoa học. Trong các bài học trước, ta đã dùng vectơ để biểu diễn các đại lượng lực, vận tốc và dùng phép toán vectơ để tính hợp lực và tổng hợp vận tốc. Bài học này tiếp tục xây dựng khái niệm tích vô hướng giữa hai vectơ - đối tượng toán học còn được dùng để định nghĩa khái niệm công sinh bởi một lực trong Vật lí.
1. GÓC GIỮA HAI VECTƠ
HĐ1. Trong Hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ 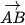 và
và 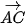 . Hãy tìm số đo các góc giữa
. Hãy tìm số đo các góc giữa 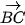 và
và 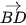 ,
, 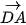 và
và 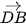 .
.
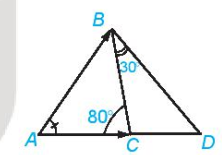
Hình 4.39
Cho hai vectơ 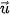 và và  khác khác 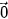 . Từ một điểm A tuỳ ý, vẽ các vectơ . Từ một điểm A tuỳ ý, vẽ các vectơ 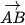 = = 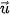 và và 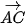 = = (H.4.40). Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ (H.4.40). Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ 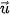 và và  hay đơn giản là góc giữa hai vectơ hay đơn giản là góc giữa hai vectơ 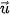 , ,  , kí hiệu là ( , kí hiệu là (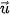 , ,  ). ). |
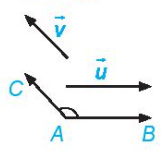
Hình 4.40
Chú ý
• Quy ước rằng góc giữa hai vectơ 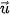 và
và 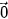 có thể nhận một giá trị tuỳ ý từ 0° đến 180.
có thể nhận một giá trị tuỳ ý từ 0° đến 180.
• Nếu (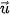 ,
,  )= 90° thì ta nói rằng
)= 90° thì ta nói rằng 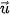 và
và  vuông góc với nhau, kí hiệu là
vuông góc với nhau, kí hiệu là 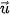 ⊥
⊥  hoặc
hoặc  ⊥
⊥ 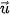 .
.
Đặc biệt 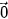 được coi là vuông góc với mọi vectơ.
được coi là vuông góc với mọi vectơ.
![]() Khi nào thì góc giữa hai vectơ bằng 0°, bằng 180° ?
Khi nào thì góc giữa hai vectơ bằng 0°, bằng 180° ?
Ví dụ 1. Cho tam giác ABC vuông tại A và B = 30°. Tính (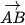 ,
, 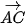 ), (CẢ, CB), (
), (CẢ, CB), (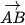 ,
, 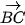 ).
).
Giải (H.4.41)
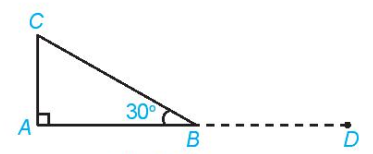
Hình 4.41
Ta có: (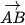 ,
, 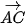 )=
)= 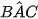 = 90°, (
= 90°, (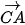 ,
, 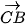 )=
)= 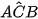 = 60°, (
= 60°, (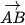 ,
, 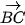 )=(
)=(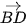 ,
, 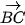 ) =
) = 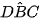 = 150°.
= 150°.
Luyện tập 1. Cho tam giác đều ABC. Tính (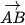 ,
, 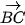 ).
).
Trang 61
2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
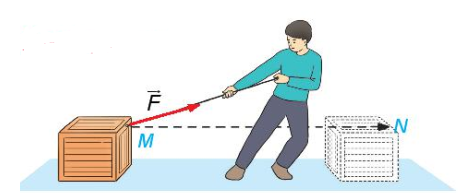
Hình 4.42
Trong Vật lí, nếu lực 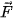 không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ M tới N, thì công A của lực
không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ M tới N, thì công A của lực 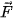 được tính theo công thức:
được tính theo công thức:
A = |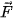 | ⋅ |
| ⋅ | | ⋅ cos(
| ⋅ cos(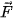 ,
,  ),
),
trong đó |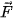 | là độ lớn của lực
| là độ lớn của lực 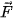 (theo đơn vị Newton);
(theo đơn vị Newton);
| | là độ dài của vectơ
| là độ dài của vectơ  (theo đơn vị mét);
(theo đơn vị mét);
(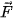 ,
,  ) là góc giữa hai vecto
) là góc giữa hai vecto 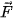 và
và  .
.
Toán học gọi giá trị A (không kể đơn vị đo) trong biểu thức nói trên là tích vô hướng của hai vecto 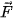 và
và  .
.
Tích vô hướng của hai vectơ 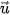 và và 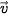 là một số, kí hiệu là là một số, kí hiệu là 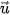 ⋅ ⋅ 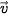 , được xác định bởi công thức sau: , được xác định bởi công thức sau: 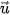 ⋅ ⋅ 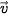 = | = |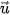 | ⋅ | | ⋅ |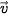 | ⋅ cos( | ⋅ cos(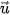 , ,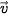 ). ). |
![]() Khi nào thì tích vô hướng của hai vectơ
Khi nào thì tích vô hướng của hai vectơ 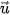 ,
, 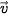 là một số dương? Là một số âm?
là một số dương? Là một số âm?
Chú ý
•  ⊥
⊥  ⇔
⇔  ⋅
⋅ 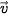 =0.
=0.
•  ⋅
⋅  và còn được viết là
và còn được viết là 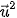 và được gọi là bình phương vô hướng của vectơ
và được gọi là bình phương vô hướng của vectơ  . Ta có
. Ta có 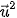 = |
= | | ⋅ |
| ⋅ | | ⋅ cos0° =
| ⋅ cos0° = 
Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.

![]() Khi nào thì
Khi nào thì 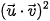 =
= 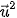 ⋅
⋅ 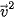 .
.
Ví dụ 2. Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng sau: 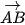 ⋅
⋅ 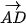 ,
, 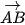 ⋅
⋅ 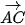 ,
, 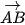 ⋅
⋅ 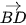 .
.
Giải. Vì ( 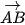 ,
,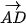 ) = 90° nên
) = 90° nên 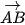 ⋅
⋅ 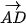 = 0.
= 0.
Hình vuông có cạnh bằng a nên có đường chéo bằng 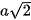 .
.
Mặt khác, (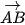 ,
,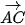 )= 45°, (
)= 45°, (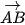 ,
,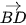 ) = 135°, do đó
) = 135°, do đó
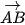 ⋅
⋅ 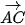 =
= 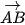 ⋅
⋅ 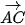 ⋅ cos 45° = a ⋅
⋅ cos 45° = a ⋅ 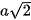 ⋅
⋅ 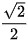 =
= 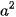 ;
;
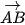 ⋅
⋅ 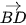 =
= 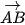 ⋅
⋅ 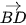 ⋅ cos 135° = a ⋅
⋅ cos 135° = a ⋅ 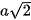 ⋅
⋅ 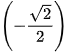 = -
= -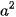
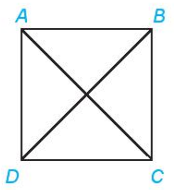
Hình 4.43
Luyện tập 2. Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính 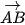 ⋅
⋅ 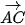 theo a, b, c.
theo a, b, c.
Hãy nhớ lại Định lí côsin.
Trang 68
3. BIỂU THỨC TOẠ ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG
HĐ2. Cho hai vectơ cùng phương  = (x; y ) và
= (x; y ) và  = (kx; ky). Hãy kiểm tra công thức
= (kx; ky). Hãy kiểm tra công thức  ⋅
⋅  = k(
= k(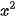 +
+ 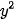 ) theo từng trường hợp sau:
) theo từng trường hợp sau:
a)  =
= 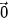 ;
;
b)  ≠
≠ 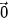 và k ≥ 0;
và k ≥ 0;
c)  ≠
≠ 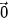 và k < 0.
và k < 0.
HĐ3. Trong mặt phẳng toạ độ Oxy, cho hai vectơ không cùng phương  =(x; y) và
=(x; y) và  =(x'; y').
=(x'; y').
a) Xác định toạ độ của các điểm A và B sao cho 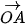 =
=  ,
, 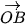 =
=  .
.
b) Tính 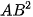 ,
, 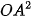 ,
, 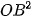 theo toạ độ của A và B.
theo toạ độ của A và B.
c) Tính 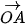 ⋅
⋅ 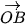 theo toạ độ của A, B.
theo toạ độ của A, B.
Tích vô hướng của hai vectơ  = (x; y) và = (x; y) và  =(x'; y') được tính theo công thức: =(x'; y') được tính theo công thức:  ⋅ ⋅  = xx' + yy' = xx' + yy' |
Để ý rằng, theo Định lí côsin, ta có: 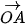 ⋅
⋅ 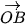 =
= 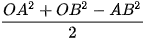 .
.

Nhận xét
• Hai vectơ  và
và  vuông góc với nhau khi và chỉ khi xx'+ yy' = 0.
vuông góc với nhau khi và chỉ khi xx'+ yy' = 0.
• Bình phương vô hướng của  (x; y) là
(x; y) là 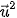 =
= 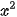 +
+ 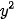 .
.
• Nếu  ≠
≠ 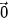 và
và  =
= 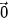 thì cos(
thì cos( ,
,  ) =
) = 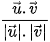 =
= 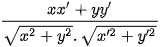 .
.
Ví dụ 3. Trong mặt phẳng toạ độ Oxy, tính tích vô hưởng của các cặp vectơ sau.
a)  = (2; -3) và
= (2; -3) và  = (5; 3);
= (5; 3);
b) Hai vectơ đơn vị 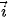 và
và 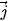 tương ứng của các trục Ox, Oy.
tương ứng của các trục Ox, Oy.
Giải
a) Ta có:  ⋅
⋅  = 2 ⋅ 5 + (-3) ⋅ 3 = 10 - 9 = 1.
= 2 ⋅ 5 + (-3) ⋅ 3 = 10 - 9 = 1.
b) Vì 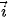 = (1; 0) và
= (1; 0) và 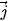 = (0; 1) nên
= (0; 1) nên 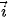 ⋅
⋅ 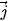 = 1 ⋅ 0 + 0 ⋅ 1 = 0.
= 1 ⋅ 0 + 0 ⋅ 1 = 0.
Luyện tập 3. Tính tích vô hướng và góc giữa hai vectơ  = (0; -5),
= (0; -5),  = (
= (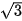 ; 1).
; 1).
HD4. Cho ba vectơ  = (
= (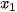 ;
; 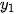 ),
),  = (
= (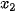 ;
; 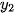 ),
), 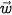 = (
= (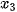 ;
; 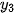 ).
).
a) Tính  ⋅ (
⋅ ( +
+ 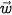 ),
),  ⋅
⋅  +
+  ⋅
⋅ 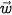 theo toạ độ của các vectơ
theo toạ độ của các vectơ  ,
,  ,
, 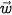 .
.
b) So sánh  ⋅ (
⋅ ( +
+ 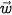 ) và
) và  ⋅
⋅  +
+  ⋅
⋅ 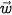 .
.
c) So sánh  ⋅
⋅  và
và  ⋅
⋅  .
.
Trang 69
| Tính chất của tích vô hướng Với ba vectơ  , ,  , , 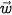 bất kì và mọi số thực k, ta có: bất kì và mọi số thực k, ta có:•  ⋅ ⋅  = =  ⋅ ⋅  (tính chất giao hoán); (tính chất giao hoán);•  ⋅ ( ⋅ ( + + 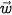 ) = ) =  ⋅ ⋅  + +  ⋅ ⋅ 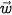 (tính chất phân phối đối với phép cộng); (tính chất phân phối đối với phép cộng);• (k  ). ).  = k( = k( ⋅ ⋅  ) = ) =  ⋅ (k ⋅ (k ). ). |
Chú ý. Từ các tính chất trên, ta có thể chứng minh được:
 (
( -
- 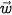 ) =
) =  ⋅
⋅  -
-  ⋅
⋅ 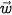 (tính chất phân phối đối với phép trừ);
(tính chất phân phối đối với phép trừ);
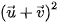 =
= 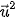 + 2
+ 2 ⋅
⋅  +
+ 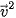 ;
; 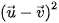 =
= 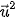 - 2
- 2 ⋅
⋅  +
+ 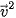 ;
;
( +
+  ) ⋅ (
) ⋅ ( -
-  ) =
) = 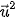 -
- 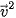 .
.
Ví dụ 4. (Ứng dụng của vectơ trong bài toán hình học)
Cho điểm M thay đổi trên đường tròn tâm O ngoại tiếp tam giác đều ABC cho trước. Chứng minh rằng 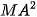 +
+ 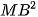 +
+ 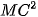 không đổi.
không đổi.
Giải
Cách 1 (Dùng toạ độ). Xét hệ trục toạ độ có gốc trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Gọi toạ độ của các điểm là A(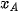 ;
; 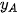 ), B(
), B(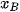 ;
; 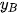 ), C(
), C(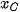 ;
; 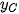 ), M(x; y). Vì tam giác ABC đều nên tâm đường tròn ngoại tiếp O(0; 0) đồng thời là trọng tâm của tam giác. Do đó
), M(x; y). Vì tam giác ABC đều nên tâm đường tròn ngoại tiếp O(0; 0) đồng thời là trọng tâm của tam giác. Do đó 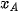 +
+ 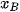 +
+ 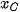 = 0 và
= 0 và 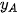 +
+ 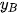 +
+ 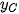 = 0.
= 0.
Vì 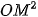 =
= 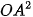 =
= 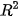 nên
nên 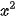 +
+ 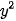 =
= 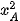 +
+ 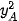 =
= 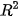 .
.
Vậy 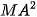 =
= 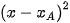 +
+ 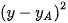 =
= 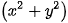 +
+ 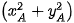 -
- 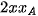 -
- 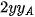 = 2
= 2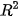 -
- 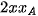 -
- 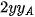 .
.
Tương tự 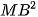 = 2
= 2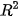 -
- 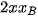 -
- 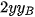 , và
, và 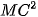 = 2
= 2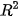 -
- 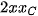 -
- 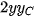 .
.
Do đó 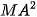 +
+ 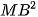 +
+ 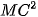 = 6
= 6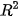 - 2x(
- 2x(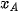 +
+ 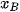 +
+ 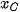 ) - 2y(
) - 2y(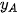 +
+ 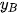 +
+ 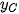 ) = 6
) = 6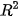 (không đổi).
(không đổi).
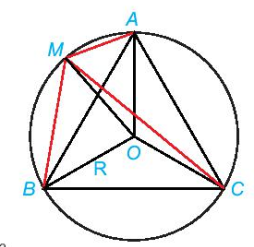
Hình 4.44
Cách 2 (Dùng tích vô hướng). (H.4.44)
Vì tam giác ABC đều nên tâm O của đường tròn ngoại tiếp đồng thời là trọng tâm của tam giác. Vậy 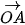 +
+ 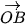 +
+ 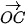 =
= 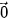 .
.
Giả sử (O) có bán kính R. Ta có: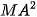 +
+ 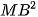 +
+ 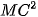 =
= 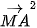 +
+ 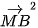 +
+ 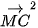
= 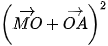 +
+ 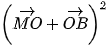 +
+ 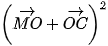
= 3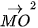 + 2
+ 2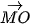 ⋅
⋅ 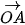 + 2
+ 2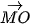 ⋅
⋅ 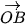 + 2
+ 2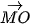 ⋅
⋅ 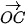 +
+ 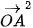 +
+ 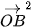 +
+ 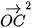
= 3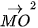 + 2
+ 2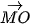 ⋅ (
⋅ (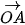 +
+ 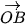 +
+ 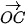 ) + 3
) + 3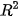 = 3
= 3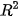 + 2
+ 2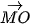 ⋅
⋅ 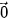 + 3
+ 3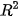 = 6
= 6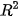 .
.
Vậy 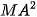 +
+ 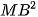 +
+ 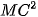 không đổi khi M thay đổi trên (O).
không đổi khi M thay đổi trên (O).
Trang 70
Luyện tập 4. Cho tam giác ABC với A(−1; 2), B(8; −1), C(8; 8). Gọi H là trực tâm của tam giác.
a) Chứng minh rằng 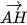 ⋅
⋅ 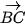 =
= 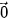 và
và 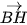 -
- 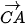 =
= 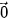 .
.
b) Tìm toạ độ của H.
c) Giải tam giác ABC.
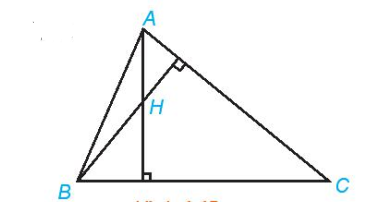
Hình 4.45
Vận dụng. Một lực 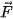 không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực
không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực 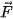 được phân tích thành hai lực thành phần là
được phân tích thành hai lực thành phần là 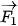 và
và 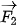 (
(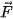 =
= 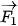 +
+ 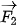 ).
).
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực 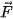 (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực
(đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực 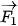 và
và 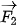 .
.
b) Giả sử các lực thành phần 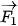 ,
, 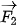 tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực
tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực 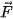 và lực
và lực 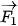 .
.
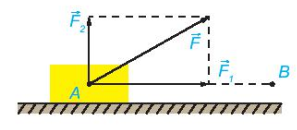
Hình 4.46
BÀI TẬP
4.21. Trong mặt phẳng toạ độ Oxy, hãy tính góc giữa hai vectơ 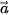 và
và 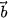 trong mỗi trường hợp sau.
trong mỗi trường hợp sau.
a) 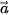 = (-3; 1),
= (-3; 1), 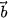 =(2; 6);
=(2; 6);
b) 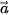 = (3; 1),
= (3; 1), 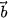 = (2; 4);
= (2; 4);
c) 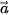 = (-
= (-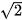 ; 1),
; 1), 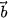 = (2; -
= (2; -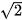 ).
).
4.22. Tìm điều kiện của 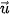 ,
, 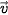 để:
để:
a) 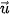 ⋅
⋅ 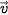 = |
= |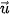 | ⋅ |
| ⋅ |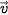 |; b)
|; b) 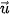 ⋅
⋅ 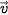 = -|
= -|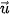 | ⋅ |
| ⋅ |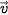 |
|
4.23. Trong mặt phẳng toạ độ Oxy, cho hai điểm A(1; 2), B(−4,3 ). Gọi M(t; 0) là một điểm thuộc trục hoành.
a) Tính 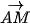 ⋅
⋅ 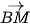 theo t.
theo t.
b) Tìm t để 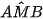 = 90°.
= 90°.
4.24. Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(-4; 1), B(2; 4), C(2; -2).
a) Giải tam giác ABC.
b) Tìm toạ độ trực tâm H của tam giác ABC.
4.25. Chứng minh rằng với mọi tam giác ABC, ta có:
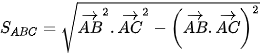 .
.
4.26. Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M, ta có:
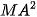 +
+ 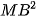 +
+ 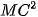 = 3
= 3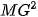 +
+ 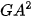 +
+ 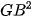 +
+ 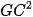 .
.

























