Trang 33

Lượng giác được phát triển từ nhu cầu tính toán góc và khoảng cách trong rất nhiều lĩnh vực như thiên văn học, lập bản đồ, bản vẽ thiết kế, khảo sát và tìm tầm bắn của pháo binh.
Ở lớp 9, em đã biết tỉ số lượng giác của một góc nhọn. Chương này mở rộng khái niệm đó cho một góc bất kì từ 0° đến 180°.
| THUẬT NGỮ • Giá trị lượng giác của một góc nhỏ • Hai góc bù nhau | KIẾN THỨC, KĨ NĂNG |
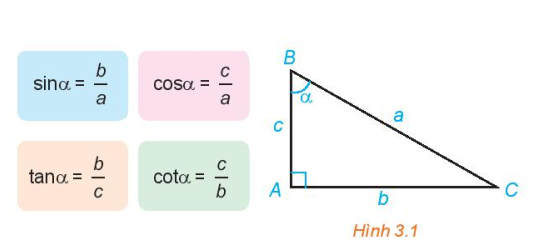
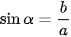
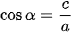
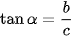
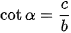
Hình 3.1

Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao?
Trang 34
1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC
Trong mặt phẳng toạ độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành (H.3.2) được gọi là nửa đường tròn đơn vị.
Cho trước một góc α, 0° ≤ α ≤180. Khi đó, có duy nhất điểm M(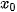 ,
, 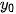 ) trên nửa đường tròn đơn vị nói trên để
) trên nửa đường tròn đơn vị nói trên để 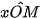 = α.
= α.
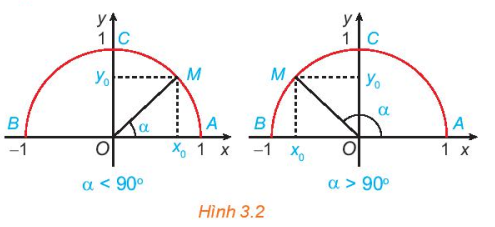
α < 90°
α > 90°
Hình 3.2
HĐ1. a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
• α = 90°; • α < 90°; • α >90°.
b) Khi 0° < α < 90°, nêu mối quan hệ giữa cos α, sin α với hoành độ và tung độ của điểm M.
Mở rộng khái niệm tỉ số lượng giác của một góc nhọn cho một góc bất kì từ 0° đến 180°, ta có định nghĩa sau:
Với mỗi góc α (0° ≤ α ≤180°), gọi M(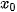 ;
; 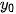 ) là điểm trên nửa đường tròn đơn vị sao cho
) là điểm trên nửa đường tròn đơn vị sao cho 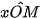 = α. Khi đó:
= α. Khi đó:
• sin của góc α là tung độ 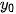 của điểm M, được kí hiệu là sin α;
của điểm M, được kí hiệu là sin α;
• côsin của góc α là hoành độ 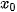 của điểm M, được kí hiệu là cos α;
của điểm M, được kí hiệu là cos α;
• Khi α # 90° (hay là 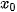 ≠ 0), tang của α là
≠ 0), tang của α là 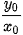 , được kí hiệu là tan α;
, được kí hiệu là tan α;
• Khi α # 0° và α # 180° (hay là 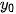 # 0), côtang của α là
# 0), côtang của α là 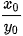 , được kí hiệu là cot α.
, được kí hiệu là cot α.
Từ định nghĩa trên, ta có:
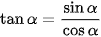 (α # 90°); (α # 90°); 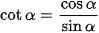 (α ≠ 0°và α ≠ 180°); (α ≠ 0°và α ≠ 180°); 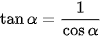 (α ∉ {0°;90°;180°}) (α ∉ {0°;90°;180°}) |
Sau đây là bảng giá trị lượng giác (GTLG) của một số góc đặc biệt mà em nên nhớ.
| GTLG/α | 0° | 30° | 45° | 60° | 90° | 180° |
| sin α | 0 | 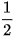 | 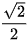 | 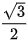 | 1 | 0 |
| cos α | 1 | 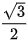 | 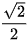 | 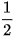 | 0 | -1 |
| tan α | 0 | 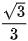 | 1 | 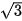 | || | 0 |
| cot α | || | 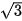 | 1 | 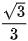 | 0 | || |
Bảng 3.1
Trong bảng, kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.

Trang 35
Ví dụ 1. Tìm các giá trị lượng giác của góc 135°.
Giải (H.3.3)
Gọi M là điểm trên nửa đường tròn đơn vị sao cho 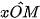 =135°. Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
=135°. Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Vì 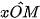 = 135° nên
= 135° nên 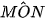 = 45°,
= 45°, 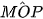 = 45°. Vậy các tam giác MON, MOP là vuông cân với cạnh huyền OM = 1.
= 45°. Vậy các tam giác MON, MOP là vuông cân với cạnh huyền OM = 1.
Từ đó, ta có ON = OP = 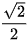 . Mặt khác, điểm M nằm bên trái trục tung nên có toạ độ là
. Mặt khác, điểm M nằm bên trái trục tung nên có toạ độ là
Theo định nghĩa, ta có:
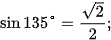
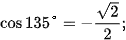
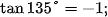
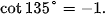
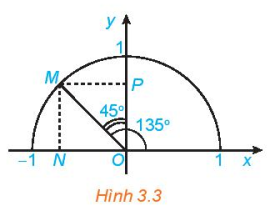
Hình 3.3
Luyện tập 1. Tìm các giá trị lượng giác của góc 120° (H.3.4).
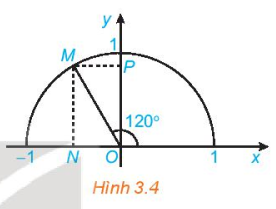
Hình 3.4
Ta có thể sử dụng máy tính cầm tay để tính (đúng hoặc gần đúng) các giá trị lượng giác của một góc và tính góc khi biết giá trị lượng giác của góc đó.

Chẳng hạn, với một loại máy tính cầm tay, sau khi mở máy ta bấm phím ![]() (SETUP) rồi bấm phím
(SETUP) rồi bấm phím  để chọn đơn vị đo góc là “độ". Sau đó tính giá trị lượng giác của góc hoặc tính góc khi biết giá trị lượng giác của góc đó.
để chọn đơn vị đo góc là “độ". Sau đó tính giá trị lượng giác của góc hoặc tính góc khi biết giá trị lượng giác của góc đó.
• Tính giá trị lượng giác của một số góc:
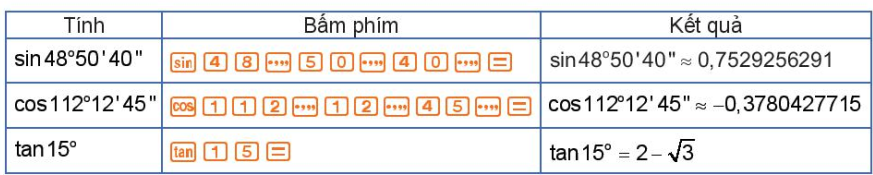
| Tính | Bấm phím | Kết quả |
| sin 48°50'40" | sin 48°50'40" ≈ 0,7529256291 | |
| cos 112°12'45" | cos 112°12'45" ≈ -0,3780427715 | |
| tan 15° | tan 15° = 2 - √3 |
• Tìm góc khi biết một giá trị lượng giác của góc đó:

| Tìm x, biết | Bấm phím | Kết quả |
| sin x = 0,3456 | x ≈ 20°13'7" |
Chú ý
• Khi tìm x biết sin x, máy tính chỉ đưa ra giá trị x ≤ 90.
• Muốn tìm x khi biết cos x, tan x, ta cũng làm tương tự như trên, chỉ thay phím  sin tương ứng bởi phím
sin tương ứng bởi phím  cos,
cos,  tan.
tan.
Trang 36
2. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU
Ở lớp 9, em đã biết mối quan hệ giữa tỉ số lượng giác của hai góc phụ nhau. Trong mục này, em hãy tìm mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau.
Đối với một góc α tuỳ ý (0° ≤ α ≤180°), gọi M, M' là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc bù nhau α và 180° – α (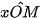 = α,
= α, 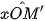 = 180° - α (H.3.5).
= 180° - α (H.3.5).
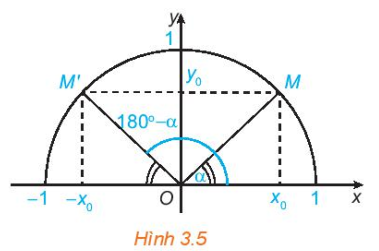
Hình 3.5
HĐ2. Nêu nhận xét về vị trí của hai điểm M, M' đối với trục Oy. Từ đó, nêu các mối quan hệ giữa sinα và sin(180° – α), giữa cosα và cos(180° - α).
| Đối với hai góc bù nhau, α và 180° -α, ta có: • sin(180° - α) = sinα; • cos (180° - α)= - cos α • tan (180° - α)= - tanα (α # 90°); • cot (180° - α) = - cotα (0° < α < 180°). |
Ví dụ 2. Tính các giá trị lượng giác của các góc 120°, 135°, 150°.
Giải
Do các góc 120°, 135°, 150° tương ứng bù với các góc 60°,45°,30° nên từ Bảng 3.1, ta cũng có bảng các giá trị lượng giác sau:
| GTLG/α | 120° | 135° | 150° |
| sin α | 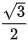 | 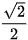 | 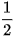 |
| cos α | 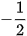 | 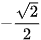 | 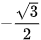 |
| tan α | 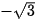 | -1 | 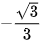 |
| cot α | 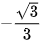 | -1 | 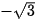 |
Bảng 3.2
Hai góc bù nhau có sin bằng nhau; có côsin, tang, côtang đối nhau.

Luyện tập 2. Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau α và 90° - α ( = α,
= α, 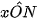 = 90° - α). Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa cosα và sin(90° - α).
= 90° - α). Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa cosα và sin(90° - α).
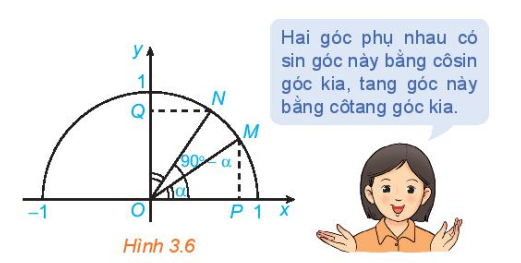
Hình 3.6
Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Trang 37
Vận dụng. Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
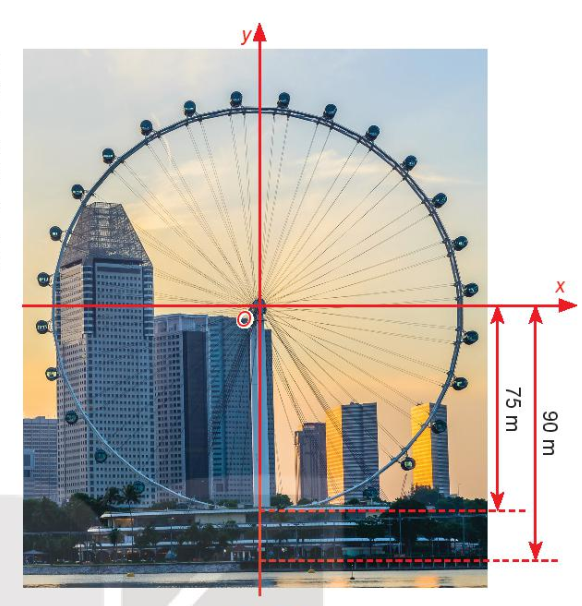
Hình 3.7
BÀI TẬP
3.1. Không dùng bảng số hay máy tính cầm tay, tính giá trị của các biểu thức sau:
a) (2sin 30° + cos135° - 3tan150°) ⋅ (cos180° - cot60°);
b) 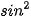 90° +
90° + 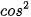 120° +
120° + 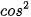 0° -
0° - 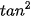 60° +
60° + 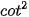 135°;
135°;
c) cos60° ⋅ sin30° + 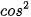 30°.
30°.
Chú ý. 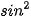 α =
α = 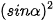 ,
, 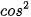 α =
α = 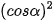 ,
, 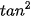 α =
α =  ,
, 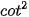 a =
a = 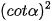
3.2. Đơn giản các biểu thức sau:
a) sin100° + sin80° + cos16° + cos164°;
b) 2sin(180° – α) ⋅ cotα – cos(180° – α) ⋅ tanα ⋅ cot(180° – α), với 0° < α <90.
3.3. Chứng minh các hệ thức sau:
a) 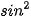 α+
α+ 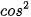 α = 1;
α = 1;
b) 1+ 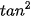 α =
α = 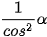 (α # 90°);
(α # 90°);
c) 1+ 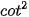 α =
α = 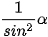 (0° < α < 180°).
(0° < α < 180°).
3.4. Cho góc α (0° < α < 180°) thoả mãn tanα = 3.
Tính giá trị của biểu thức: