Ví dụ 1
Lập các tỉ lệ thức có thể được từ bốn số: 15; 18; 20; 24.
Giải. Từ bốn số đã cho ta lập được đẳng thức: 15 . 24 = 18 . 20 (vì đều bằng 360).
Từ đẳng thức này ta lập được bốn tỉ lệ thức sau: 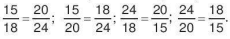
Ví dụ 2
Tìm x và y sao cho 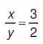 và x+y=15.
và x+y=15.
Giải. Từ 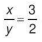 suy ra
suy ra 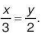
Theo tính chất của dãy tỉ số bằng nhau, ta có 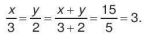
Suy ra x = 3 . 3 9 và y = 3 . 2 = 6.
Ví dụ 3
Tính độ dài các cạnh của một tam giác, biết độ dài các cạnh của nó tỉ lệ với 2; 3; 4 và cạnh lớn nhất dài hơn cạnh nhỏ nhất 6 cm.
Giải. Gọi x, y, z (cm) lần lượt là độ dài ba cạnh của tam giác (theo thứ tự từ nhỏ đến lớn). Theo đề bài, ta có 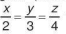 và z-x=6.
và z-x=6.
Theo tính chất của dãy tỉ số bằng nhau, ta có: 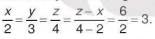
Suy ra x = 3 . 2 = 6, y = 3 . 3 = 9 và z = 3 . 4 = 12. Vậy độ dài ba cạnh của tam giác đó là 6 cm, 9 cm và 12 cm.
BÀI TẬP
6.11. Lập các tỉ lệ thức có thể được từ đẳng thức 3x – 4y (x,y  0).
0).
6.12. Hãy lập tất cả các tỉ lệ thức có thể được từ bốn số: 5; 10; 25; 50.
6.13. Tìm x và y, biết: 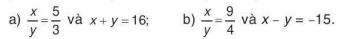
6.14. Tỉ số của số học sinh của hai lớp 7A và 7B là 0,95. Hỏi mỗi lớp có bao nhiêu học sinh, biết số học sinh của một lớp nhiều hơn lớp kia là 2 em?
6.15. Người ta định làm một con đường trong 15 ngày. Một đội công nhân 45 người làm trong 10 ngày mới được một nửa công việc. Hỏi phải bổ sung thêm bao nhiêu người nữa để có thể hoàn thành công việc đúng hạn (biết năng suất lao động của mỗi người như nhau)?
6.16. Tìm ba số x, y, z, biết rằng: 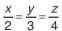 và x + 2y - 3z = -12.
và x + 2y - 3z = -12.



































