| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| - Đại lượng tỉ lệ thuận - Hệ số tỉ lệ | Nhận biết hai đại lượng tỉ lệ thuận. Giải một số bài toán đơn giản về đại lượng tỉ lệ thuận. |
Bột sắn dây được làm từ củ sắn dây, là một loại thực phẩm có nhiều tác dụng tốt với sức khoẻ. Ông An nhận thấy cứ 4,5 kg củ sắn dây tươi thì thu được khoảng 1 kg bột. Hỏi với 3 tạ củ sắn dây tươi, ông An sẽ thu được khoảng bao nhiêu kilôgam bột sắn dây?
1. ĐẠI LƯỢNG TỈ LỆ THUẬN
Nhận biết đại lượng tỉ lệ thuận Một xe ô tô di chuyển với vận tốc không đổi 60 km/h. Gọi s (km) là quãng đường ô tô đi được trong khoảng thời gian t (h).

HĐ1 Thay mỗi dấu "?" trong bảng sau bằng số thích hợp.
| t(h) | 1 | 1,5 | 2 | 3 |
| s(km) | ? | ? | ? | ? |
HĐ2 Viết công thức tính quãng đường s theo thời gian di chuyển tương ứng t.
| Nếu đại lượng y liên hệ với đại lượng x theo công thức y = ax (a là hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ a. |
Trong HĐ2, quãng đường s có tỉ lệ thuận với thời gian t không? Thời gian t có tỉ lệ thuận với quãng đường s không?
Chú ý. Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ a thì x tỉ lệ thuận với y theo hệ số tỉ lệ 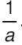 . Khi đó ta nói x và y là hai đại lượng tỉ lệ thuận.
. Khi đó ta nói x và y là hai đại lượng tỉ lệ thuận.
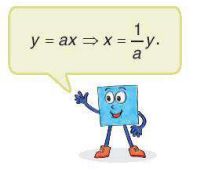
Ví dụ 1
Biết rằng x và y là hai đại lượng tỉ lệ thuận và x = 2 khi y = -4.
a) Tìm hệ số tỉ lệ a trong công thức y = ax. Từ đó viết công thức tính y theo x;
b) Tìm giá trị của y khi x = 3;
c) Tìm giá trị của x khi y = 0,8
Giải
a) Ta có a = 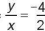 = -2. Do đó y = -2x.
= -2. Do đó y = -2x.
b) Khi x = 3 thì y = -2 . 3 = -6.
c) Từ y = -2x suy ra 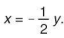 Do đó khi y = 0,8 thì x =
Do đó khi y = 0,8 thì x = 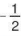 . 0,8 = 0,4.
. 0,8 = 0,4.
Ví dụ 2
Cho y tỉ lệ thuận với x theo hệ số tỉ lệ a = 5.
a) Thay mỗi dấu *?" trong bảng bên bằng số thích hợp.
b) Tính 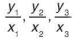 và so sánh với hệ số tỉ lệ a.
và so sánh với hệ số tỉ lệ a.

Giải

a) Theo đề bài, y = 5x. Do đó ta có bảng bên.
b) Ta có 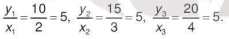
Vậy 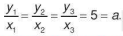
Nhận xét. Nếu đại lượng y tỉ lệ thuận với i đại lượng x thì:
Tỉ số hai giá trị tương ứng của chúng luôn không đổi (và bằng hệ số tỉ lệ):
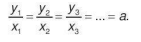
Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia:
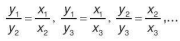
Luyện tập 1
Theo Viện Dinh dưỡng Quốc gia, cứ trong 100 g đậu tương (đậu nành) thì có 34 g protein. Khối lượng protein trong đậu tương có tỉ lệ thuận với khối lượng đậu tương không? Nếu có thì hệ số tỉ lệ là bao nhiêu?
Vận dụng. Em hãy giải bài toán mở đầu.
2. MỘT SỐ BÀI TOÁN VỀ ĐẠI LƯỢNG TỈ LỆ THUẬN
Trong mục này ta sẽ vận dụng tính chất của đại lượng tỉ lệ thuận để giải một số bài toán về đại lượng tỉ lệ thuận.
Giải toán về đại lượng tỉ lệ thuận
Để giải toán về đại lượng tỉ lệ thuận, ta cần nhận biết hai đại lượng tỉ lệ thuận trong bài toán. Từ đó ta có thể lập các tỉ số bằng nhau và dựa vào tính chất của dãy tỉ số bằng nhau để tìm các yếu tố chưa biết.
Ví dụ 3
Một công ty may quần áo bảo hộ lao động có hai xưởng may, xưởng thứ nhất có 25 công nhân, xường thứ hai có 30 công nhân. Mỗi ngày xưỡng thứ hai may được nhiều hơn xưởng thứ nhất 20 bộ quần áo. Hỏi trong một ngày, mỗi xưởng may được bao nhiêu bộ quần áo (biết năng suất của mỗi công nhân là như nhau)?
Giải
Gọi số bộ quần áo may được trong một ngày của xưởng thứ nhất và xưỡng thứ hai lần lượt là x, y (bộ).
Ta có y - x = 20. Vì năng suất của mỗi công nhân là như nhau nên số bộ quần áo may được tỉ lệ thuận với số công nhân. Do đó ta có: 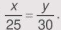
Theo tính chất của dãy tỉ số bằng nhau, ta có 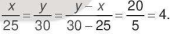
Suy ra: x = 4 . 25 = 100 và y = 4 . 30 = 120.
Vậy mỗi ngày xưởng thứ nhất may được 100 bộ quần áo và xưởng thứ hai may được 120 bộ quần áo.
Luyện tập 2
Hai thanh kim loại đồng chất có thể tích tương ứng là 10 cm³ và 15 cm³. Hỏi mỗi thanh nặng bao nhiêu gam, biết rằng một thanh nặng hơn thanh kia 40 g?

Ví dụ 4
Trong một đợt tặng đồ dùng học tập cho học sinh vùng cao, có 635 quyển vở được chia cho ba lớp 7A, 7B, 7C tỉ lệ thuận với số học sinh của mỗi lớp. Hỏi mỗi lớp được tặng bao nhiêu quyển vở, biết sĩ số của ba lớp 7A, 78, 7C lần lượt là 40; 42 và 45 học sinh.
Giải
Gọi x, y, z (quyền) lần lượt là số vỡ ba lớp 7A, 7B, 7C được tặng.
Theo đề bài, ta có x + y + z = 635 và 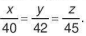
Luyện tập 3
Hãy chia 1 tấn gạo thành ba phần có khối lượng tỉ lệ thuận với 2; 3; 5.
BÀI TẬP
6.17. Cho biết x và y là hai đại lượng tỉ lệ thuận. Thay mỗi dấu "?" trong bảng sau bằng số thích hợp.
| x | 2 | 4 | 5 | ? | ? | ? |
| y | -6 | ? | ? | 9 | 18 | 1,5 |
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y.
6.18. Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ thuận không?
| x | 5 | 9 | 15 | 24 |
| y | 15 | 27 | 45 | 72 |
| x | 4 | 8 | 16 | 25 |
| y | 8 | 16 | 30 | 50 |
6.19. Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ a, x tỉ lệ thuận với z theo hệ số tỉ lệ b. Hỏi y có tỉ lệ thuận với z không? Nếu có thì hệ số tỉ lệ là bao nhiêu?
6.20. Hai bể nước hình hộp chữ nhật có chiều dài và chiều rộng tương ứng bằng nhau, nhưng chiều cao của bể thứ nhất bằng 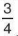 chiều cao của bể thứ hai. Để bơm đầy nước vào bể thứ nhất mất 4,5 giờ. Hỏi phải mất bao nhiêu thời gian để bơm đầy nước vào bể thứ hai (nếu dùng máy bơm có cùng công suất)?
chiều cao của bể thứ hai. Để bơm đầy nước vào bể thứ nhất mất 4,5 giờ. Hỏi phải mất bao nhiêu thời gian để bơm đầy nước vào bể thứ hai (nếu dùng máy bơm có cùng công suất)?
6.21. Để chuẩn bị cho học sinh làm thí nghiệm, cô Hương chia 1,5 lít hoá chất thành ba phần tỉ lệ thuận với 4; 5; 6 và đựng trong ba chiếc lọ. Hỏi mỗi chiếc lọ đựng bao nhiêu lít hoá chất đó?

























