| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| Đại lượng tỉ lệ nghịch Hệ số tỉ lệ | - Nhận biết hai đại lượng tỉ lệ nghịch. - Giải một số bài toán đơn giản về đại lượng tỉ lệ nghịch. |

Bốn người thợ cùng làm sẽ xây xong một bức tường trong 9 ngày. Hỏi 6 người thợ cùng làm sẽ xây xong bức tường đó trong bao nhiêu ngày (biết năng suất lao động của mỗi người thợ là như nhau)?
1. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
Nhận biết đại lượng tỉ lệ nghịch
Một ô tô đi từ thành phố A đến thành phố B trên quãng đường 180 km. Gọi t (h) là thời gian để ô tô đi từ A đến B với vận tốc v (km/h).

HĐ1 Thay mỗi dấu "?" trong bảng sau bằng số thích hợp.
| v(km/h) | 40 | 50 | 60 | 80 |
| t(h) | ? | ? | ? | ? |
HĐ2 Viết công thức tính thời gian ở theo vận tốc tương ứng v.
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = 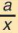 = (a là một hàng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
= (a là một hàng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Trong HĐ2, thời gian 1 có tỉ lệ nghịch với vận tốc v không? Vận tốc v có tỉ lệ nghịch với thời gian t không?
Chú ý. Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ a và ta nói hai đại lượng x và y tỉ lệ nghịch với nhau.
Ví dụ 1
Biết rằng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = -4.
a) Tìm hệ số tỉ lệ a trong công thức y= 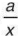 . Từ đó viết công thưc tính y theo x.
. Từ đó viết công thưc tính y theo x.
b) Tìm giá trị của y khi x = 4.
c) Tìm giá trị của x khi y = 0,5. a x
Giải
a) Ta có a = xy = 2 . (-4) = -8. Do đó y = 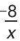
Ví dụ 2 Cho y tỉ lệ nghịch với x theo hệ số tỉ lệ a = 12.
a) Thay mỗi dấu "?" trong bảng bên bằng số thích hợp.

b) Tính 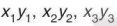 , và so sánh với hệ số tỉ lệ a.
, và so sánh với hệ số tỉ lệ a.
Giải
a) Theo đề bài ta có y= 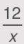 Do đó ta có bảng bên:
Do đó ta có bảng bên:

b) Ta có: 
Như vậy 
Nhận xét. Nếu hai đại lượng y và x tỉ lệ nghịch với nhau thì:
• Tích hai giá trị tương ứng của chúng luôn không đổi (và bằng hệ số tỉ lệ):
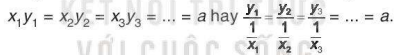
Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia:
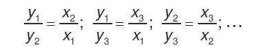
Luyện tập 1 Chiều dài và chiều rộng của các hình chữ nhật có cùng diện tích bằng 12 cm² có phải là hai đại lượng tỉ lệ nghịch không? Nếu có thì hệ số tỉ lệ là bao nhiêu?
Vận dụng 1
a) Một cửa hàng bán gạo cần đóng 300 kg gạo thành các túi gạo có khối lượng như nhau. Thay mỗi dấu "?" trong bằng sau bằng số thích hợp.
| Lượng gạo trong mỗi túi (kg) | 5 | 10 | ? | ? |
| Số túi tương ứng | ? | ? | 15 | 12 |
b) Số túi gạo và số kilôgam gạo trong mỗi túi có phải là hai đại lượng tỉ lệ nghịch không? Nếu có thì hệ số tỉ lệ là bao nhiêu?
2. MỘT SỐ BÀI TOÁN VỀ ĐẠI LƯỢNG TỈ LỆ NGHỊCH
Trong mục này ta sẽ vận dụng tính chất của đại lượng tỉ lệ nghịch để giải một số bài toán về đại lượng tỉ lệ nghịch.
Giải toán về đại lượng tỉ lệ nghịch
Để giải toán về đại lượng tỉ lệ nghịch, ta cần nhận biết được hai đại lượng tỉ lệ nghịch trong bài toán. Từ đó ta có thể lập các tỉ số bằng nhau và dựa vào tính chất của dãy tỉ số bằng nhau để tìm các yếu tố chưa biết.
Ví dụ 3
Hãy giải bài toàn mở đầu.
Giải
Gọi x (ngày) là thời gian để 6 người thợ cùng xây xong bức tường.
Vì năng suất lao động của mỗi người thợ là như nhau nên số người thợ và thời gian để họ xây xong bức tường là hai đại lượng tỉ lệ nghịch. Do đó, ta có 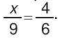
Suy ra x=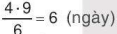
Vậy thời gian để 6 người thợ cùng xây xong bức tường là 6 ngày.
Luyện tập 2
Một nhà thầu ước tính rằng có thể hoàn thành một hợp đồng xây dựng trong 12 tháng với 280 công nhân. Nếu được yêu cầu phải hoàn thành hợp đồng trong 10 tháng thì nhà thầu đó phải thuê bao nhiêu công nhân (biết năng suất lao động của mỗi công nhân là như nhau)?
Ví dụ 4
Một người mua 65 quả trứng gà gồm ba loại: loại I giá 4 nghìn đồng một quả, loại II giá 3 nghìn đồng một quả và loại III giá 2 nghìn đồng một quả. Hỏi người đó mua bao nhiêu quả trứng mỗi loại, biết rằng số tiền mà người đó phải trả cho mỗi loại trứng là như nhau?
Giải
Gọi x, y, z lần lượt là số quả trứng gà loại I, loại II và loại III. Ta có x+y+z=65.
Vì số tiền mà người đó phải trả cho mỗi loại trứng là như nhau nên
4x=3y=2z hay ![]()
Theo tính chất của dãy tỉ số bằng nhau, ta có
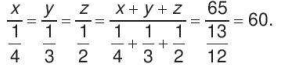
Suy ra ![]()
Vậy số trứng gà loại I, loại II, loại III lần lượt là 15 quả; 20 quả và 30 quả.
Chú ý. Trong thực hành, để tiện lợi từ dây đẳng thức 4x = 3y = 2z ta thường chia 4x, 3y, 2z cho 12 (là BCNN của 4; 3; 2) để được dây tỉ số bằng nhau 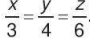 . Sau đó giải tiếp tương tự như trên.
. Sau đó giải tiếp tương tự như trên.
Luyện tập 3
Bạn An mua tổng cộng 34 quyền vỡ gồm ba loại: loại 120 trang giá 12 nghìn đồng một quyền, loại 200 trang giá 18 nghìn đồng một quyển và loại 240 trang giá 20 nghìn đồng một quyền. Hỏi Ân mua bao nhiêu quyền vỡ mỗi loại, biết rằng số tiền bạn ấy dành để mua mỗi loại vở là như nhau?
BÀI TẬP
6.22. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Thay mỗi dầu "?" trong bảng sau bằng
| x | 2 | 4 | 5 | ? | ? | ? |
| y | -6 | ? | ? | 3 | 10 | 0,5 |
Vậy số trứng gà loại I, loại II, loại III lần lượt là 15 quả; 20 quả và 30 quả.
6.23. Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ nghịch không?
a)
| x | 3 | 6 | 16 | 24 |
| y | 160 | 80 | 30 | 20 |
b)
| x | 4 | 8 | 25 | 32 |
| y | 160 | 80 | 26 | 20 |
6.24. Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a, x tỉ lệ nghịch với z theo hệ số tỉ lệ b. Hỏi y tỉ lệ thuận hay tỉ lệ nghịch với z và hệ số tỉ lệ bằng bao nhiêu?
6.25. Với cùng số tiền để mua 17 tập giấy A4 loại I có thể mua bao nhiêu tập giấy A4 loại II, biết rằng giá tiền giấy loại II chỉ bằng 85% giá tiền giấy loại I.
6.26. Ba đội máy cày làm trên ba cánh đồng cùng diện tích. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 6 ngày và đội thứ ba trong 8 ngày. Hỏi mỗi đội có mấy máy cày, biết rằng số máy của đội thứ nhất nhiều hơn số máy của đội thứ hai là 2 máy và năng suất của các máy như nhau?

























