| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| Đơn thức (một biến) Đa thức (một biến) Bậc của một đa thức Thu gọn và sắp xếp đa thức. Hệ số cao nhất Hệ số tự do Nghiệm của đa thức | Nhận biết đơn thức (một biến) và bậc của đơn thức Nhận biết đa thức (một biển) và các hạng tử của nó. Nhận biết bậc, hệ số cao nhất, hệ số tự do của một đa thức Tính giá trị của một đa thức khi biết giá trị của biển. Nhận biết nghiệm của một đa thức. |
Bài toán: Độ cao H (mét) của một vật (so với mặt đất) khi ném lên từ một điểm trên mặt đất được biểu thị bởi biểu thức H = -5x² + 15x, trong đó x (giây) là thời gian tính tử thời điểm ném vật. Hỏi sau bao lâu kể từ khi được ném lên, vật sẽ rơi trở lại mặt đất?
Dễ thấy biểu thức H có vai trò quan trọng trong bài toán trên.
Trong bài này chúng ta sẽ bước đầu tìm hiểu về các biểu thức tương tự như biểu thức H, đó là các đa thức một biến.
1. ĐƠN THỨC MỘT BIẾN
Chúng ta bắt đầu bằng những biểu thức đơn giản nhất, đó là các đơn thức một biến. Biến có thể là một chữ cái tuỳ ý. Nhưng để dễ nhận biết, ta chỉ xét các biểu thức với biến x.
Sơ lược về đơn thức một biến
1. Các biểu thức như -0,5x, 3x², 
là những ví dụ về đơn thức một biến. Chúng đều 4 là tích của một số với một luỹ thừa của x
Đơn thức một biến (gọi tắt là đơn thức) là biểu thức đại số có dạng tích của một số thực với một luỹ thừa của biến, trong đó số thực gọi là hệ số, số mũ của luỹ thừa của biến gọi là bậc của đơn thức. Chẳng hạn:
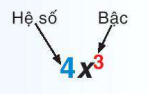
Biểu thức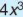 
là một đơn thức, trong đó 4 là hệ số, số mũ 3 của x là bậc của đơn thức đó.
Đơn thức –0,5x có hệ số là -0,5 và có bậc là 1 (vì x = x').
Một số khác 0 là một đơn thức bậc 0. Hệ số
Chú ý. Số 0 cũng được coi là một đơn thức. Đơn thức này không có bậc.
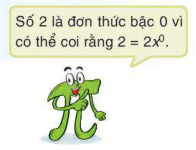
Cho biết hệ số và bậc của mỗi đơn thức sau:
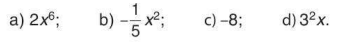
2. Với các đơn thức một biến, ta có thể:
• Cộng (hay trừ) hai đơn thức cùng bậc bằng cách cộng (hay trừ) các hệ số với nhau và giữ nguyên luỹ thừa của biến. Tổng nhận được là một đơn thức. Chẳng hạn:
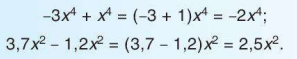
• Nhân hai đơn thức tuỳ ý bằng cách nhân hai hệ số với nhau và nhân hai luỹ thừa của biến với nhau. Tích nhận được cũng là một đơn thức. Chẳng hạn:
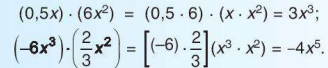
Khi nhân một đơn thức bậc 3 với một đơn thức bậc 2, ta được đơn thức bậc mấy?
Luyện tập 1
Tính:
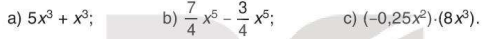
2. KHÁI NIỆM ĐA THỨC MỘT BIẾN
Đa thức một biến là gì?
• Các biểu thức 
có chung một đặc điểm: chúng đều là tổng của những đơn thức với biến x. Đó là những ví dụ về đa thức một biến.
Một cách tổng quát:
Đa thức một biến (gọi tắt là đa thức) là tổng của những đơn thức của cùng một biến; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Số 0 cũng được coi là một đa thức, gọi là đa thức không.
Chú ý. Ta thường kí hiệu đa thức bằng một chữ cái in hoa. Đôi khi còn viết thêm kí hiệu biến trong ngoặc đơn. Chẳng hạn:
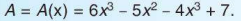
Mỗi số thực có phải là một đa thức không? Tại sao?
Ví dụ 1
Đa thức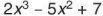 
có ba hạng tử là 
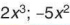và 7.
Luyện tập 2
Hãy liệt kê các hạng từ của đa thức B =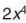 
- 3x² + x + 1.
3. ĐA THỨC MỘT BIẾN THU GỌN
Đa thức thu gọn
Xét hai đa thức 
, ta thấy:
• Trong đa thức A có hai đơn thức cùng bậc là 
.
• Trong đa thức B không có hai đơn thức nào cùng bậc.
Ta gọi các đa thức không chứa hai đơn thức nào cùng bậc là các đa thức thu gọn.
Ví dụ 2 dưới đây sẽ cho thấy: nếu cho một đa thức có chứa những đơn thức cùng bậc (đa thức chưa thu gọn) thì ta có thể đưa nó về dạng thu gọn.
Ví dụ 2
Thu gọn đa thức A =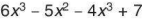 
Giải
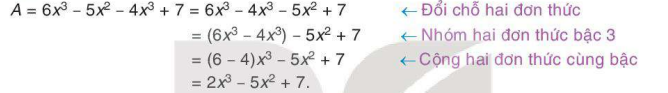
Kết quả, ta được đa thức thu gọn 2x³-5x² +7.
Luyện tập 3
Thu gọn đa thức P = 2x³ - 5x² + 4x³ + 4x + 9 + x.
4. SẮP XẾP ĐA THỨC MỘT BIẾN
* Sắp xếp đa thức theo luỹ thừa giảm của biến HỨC
Dưới đây, ta chỉ xét các đa thức khác đa thức không.
• Để thuận lợi cho việc tính toán các đa thức một biến, người ta thường viết chúng dưới dạng thu gọn và sắp xếp các hạng tử của nó theo luỹ thừa giảm của biến.
Chẳng hạn, sắp xếp các hạng tử của đa thức P =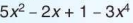 
theo luỹ thừa giảm của biến, ta được P = 
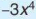+ 5x²-2x+1. • Trong đa thức P ta thấy có các đơn thức bậc 4 và bậc 2, nhưng khuyết đơn thức bậc 3. ''
Tuy nhiên khi cần, ta cũng có thể viết: P= 
+ 5x²-2x+1.
Ở đây, ta coi rằng hệ số của luỹ thừa bậc 3 là 0.
Luyện tập 4
Thu gọn (nếu cần) và sắp xếp mỗi đa thức sau theo luỹ thừa giảm của biến: a
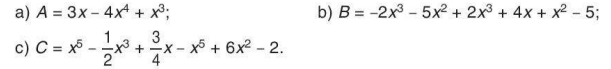
Chú ý. Người ta cũng có thể sắp xếp đa thức theo luỹ thừa tăng của biển. Chẳng hạn, ta có thể sắp xếp các hạng từ của đa thức P trên đây như sau: P = 1-2x+5x²-3x4.
5. BẬC VÀ CÁC HỆ SỐ CỦA MỘT ĐA THỨC
Bậc, hệ số cao nhất và hệ số tự do của một đa thức:
Xét đa thức P=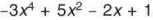 
. Đó là một đa thức thu gọn. Hãy quan sát các hạng tử (các đơn thức) của đa thức Píà trả lời các câu hỏi sau:
HĐ1 Trong đa thức P. bậc của hạng tử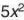 
sứ là 2 (số mũ của 
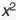). Hãy xác định tiệc của các hạng từ trong P. a
HĐ2 Trong đa thức P, hạng tử nào có bậc cao nhất? Tìm hệ số và bậc của hạng từ
HĐ3 Trong đa thức P, hạng từ nào có bậc bằng 0?
Hạng sử có bậc cao nhất và hạng tử bậc 2 có vai trò đặc biệt trong một đa thức. Ta có định nghĩa
Trong một đa thức thu gọn và khác đa thức không:
Bậc của hạng từ có bậc cao nhất gọi là bậc của đa thức đó.
Hệ số của hạng từ có bậc cao nhất gọi là hệ số cao nhất của đa thức đã
Hệ số của hạng từ bậc 0 gọi là hệ số tự do của đa thức đã
Chú ý
• Đa thức không là đa thức không có bậc.
• Trong một đa thức thu gọn, hệ số cao nhất phải khác 6 (các hệ số khác có thể bằng 0).
• Muốn tìm bậc của một đa thức chưa thu gọn, ta phải thu gọn đa thức đó
2 Một số khác 6 cũng là một đa thức. Vậy bậc của nó bằng bao nhiêu?
Ví dụ 3
Tìm bậc, hệ số cao nhất và hệ số tự do của đa thức P = 
Giải
Trước hết ta thu gọn P:
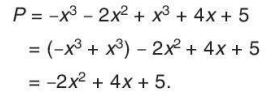
Trong dạng thu gọn của P, hạng tử có bậc cao nhất là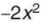 
nên bậc của P là 2, hệ số cao nhất là 2: hạng từ bậc 0 là 5 nên hệ số tự do là 5.
Luyện tập 5
Xác định bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức sau:
a)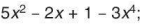
b)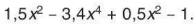
6. NGHIỆM CỦA ĐA THỨC MỘT BIẾN
Giá trị và nghiệm của một đa thức Xét đa thức
G(x) = x² - 4. Giá trị của biểu thức G(x) tại x = 3 còn gọi là giá trị của đa thức
G(x) tại x = 3 và được kí hiệu là G(3). Như vậy, ta có G(3) = 
-4 = 5. HĐ4
HĐ4 Tính các giá trị G(-2); G(-1); G(0); G(1); G(2).
HĐ5 Với giá trị nào của x thì G(x) có giá trị bằng 07
Nếu tại x = a, đa thức F(x) có giá trị bằng 0, tức là F(a) = 0, thì ta gọi a (hoặc x = a) là một nghiệm của đa thức F(x).
Ví dụ 4
a) x = -3 và x = 0 là hai nghiệm của đa thức A(x) = 2x² + 6x vì
A(0) = 0 và A(-3) = 2(-3)
+6 . (-3) = 0.
b) Đa thức B(x) = x² + 1 không có nghiệm vì tại giá trị bất kì của x, ta luôn có x² ≥ 0 nên B(x) = x² + 1 ≥ 1>0.
Nhận xét
Nếu một đa thức có hệ số tự do bằng 0 thì x = 0 là một nghiệm của đa thức đó. Chẳng hạn, trong ví dụ trên cho thấy đa thức A(x) = 2x² + 6x có hệ số tự do bằng 0 và có nghiệm x = 0.
Luyện tập 6
1. Tính giá trị của đa thức F(x) = 2x² – 3x - 2 tại x = -1; x = 0; x = 1; x = 2. Từ đó hãy tìm một nghiệm của đa thức F(x).
2. Tìm nghiệm của đa thức E(x) = x²+x.
Vận dụng
Trở lại bài toán mở đầu, hãy thực hiện các yêu cầu sau:
a) Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức H(x) = -5x² + 15x.
b) Tại sao x = 0 là một nghiệm của đa thức H(x)? Kết quả đó nói lên điều gì?
c) Tính giá trị của H(x) khi x = 1; x = 2 và x = 3 để tìm nghiệm khác 0 của H(x). Nghiệm ấy có ý nghĩa gì? Từ đó hãy trả lời câu hỏi của bài toán.
BÀI TẬP
7.5. a) Tính (2) (-4x²). Tim hệ: số và bậc của đơn thức nhận được.
c) Tính giá trị của H(x) khi x = 1; x = 2 và x = 3 để tìm nghiệm khác 0 của H(x). Nghiệm ấy có ý nghĩa gì? Từ đó hãy trả lời câu hỏi của bài toán.
BÀI TẬP
7.5.
a) Tính 
. (-4x²). Tìm hệ số và bậc của đơn thức nhận được.
b) Tính 
. Tìm hệ số và bậc của đơn thức nhận được.
7.6. Cho hai đa thức:
a ) Thu gọn và sắp xếp hai đa thức trên theo luỹ thừa giảm của biến.
b) Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức đã cho.
7.7. Cho hai đa thức:
a) Thu gọn và sắp xếp hai đa thức trên theo luỹ thừa giảm của biến.
b) Sử dụng kết quả câu a để tính P(1), P(0), Q(-1) và Q(0).
7.8. Người ta dùng hai máy bơm để bơm nước vào một bể chứa nước. Máy thứ nhất bơm mỗi giờ được 22 m³ nước. Máy thứ hai bơm mỗi giờ được 16 m³ nước. Sau khi cả hai máy chạy trong x giờ, người ta tắt máy thứ nhất và để máy thứ hai chạy thêm 0,5 giờ nữa thì bể nước đây.
Hãy viết đa thức (biến x) biểu thị dung tích của bể (m³), biết rằng trước khi bơm, trong bể có 1,5 m³ nước. Tìm hệ số cao nhất và hệ số số tự do của đa thức đó.
7.9. Viết đa thức F(x) thoả mãn đồng thời các điều kiện sau:
• Bậc của F(x) bằng 3.
• Hệ số của x² bằng hệ số của x và bằng 2.
• Hệ số cao nhất của F(x) bằng -6 và hệ số tự do bằng 3.
7.10. Kiểm tra xem:
a) x= 
có phải là nghiệm của đa thức P(x) = 4x +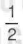 
= không?
b) Trong ba số 1; -1 và 2, số nào là nghiệm của đa thức Q(x) = x² + x - 27
7.11. Mẹ cho Quỳnh 100 nghìn đồng. Quỳnh mua một bộ dụng cụ học tập có giá 37 nghìn đồng và một cuốn sách tham khảo môn Toán với giá x (nghìn đồng).
a) Hãy tìm đa thức (biến x) biểu thị số tiền Quỳnh còn lại (đơn vị: nghìn đồng). Tìm bậc của đa thức đó.
b) Sau khi mua sách thì Quỳnh tiêu vừa hết số tiền mẹ cho. Hỏi giá tiền của cuốn sách là bao nhiêu?
EM CÓ BIẾT?
• Mỗi đa thức bậc nhất với biến x đều có thể viết dưới dạng
ax + b (a, b là các số cho trước và a ≠ 0).
Do đó ta còn gọi đa thức bậc nhất là nhị thức bậc nhất (gọi là nhị thức vì đa thức này có hai hạng tử).
• Mỗi đa thức bậc hai với biến x đều có thể viết dưới dạng
ax² + bx + c (a, b và c là các số cho trước và a ≠ 0).
Do đó ta còn gọi đa thức bậc hai là tam thức bậc hai (gọi là tam thức vì đa thức này có ba hạng tử).
