[trang 49]
BÀI 12. BỘI CHUNG. BỘI CHUNG NHỎ NHẤT
KHÁI NIỆM, THUẬT NGỮ
Bội chung
Bội chung nhỏ nhất
KIẾN THỨC, KĨ NĂNG
* Tìm bội chung, bội chung nhỏ nhất của hai hoặc ba số tự nhiên.
* Sử dụng bội chung nhỏ nhất để quy đồng mẫu các phân số và cộng, trừ phân số.
Mai cần mua đĩa giấy, cốc giấy để chuẩn bị cho một bữa tiệc sinh nhật. Đĩa và cốc được đóng thành từng gói với số lượng mỗi loại khác nhau: gói 4 cái đĩa và gói 6 cái cốc. Cửa hàng chỉ bán từng gói mà không bán lẻ. Mai muốn mua số đĩa và số cốc bằng nhau thì phải mua ít nhất bao nhiêu gói mỗi loại?

1. BỘI CHUNG VÀ BỘI CHUNG NHỎ NHẤT
Bội chung và bội chung nhỏ nhất của hai hay nhiều số
HĐ1 Tìm các tập hợp B(6), B(9).
HĐ2 Gọi BC(6, 9) là tập hợp các số vừa là bội của 6, vừa là bội của 9. Hãy viết tập BC(6, 9).
HĐ3 Tìm số nhỏ nhất khác 0 trong tập BC(6, 9).
Bội chung của hai hay nhiều số là bội của tất cả các số đó.
Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.
Ta kí hiệu:
BC(a, b) là tập hợp các bội chung của a và b;
BCNN(a, b) là bội chung nhỏ nhất của a và b.
Chú ý. Ta chỉ xét bội chung của các số khác 0.
Ví dụ 1
Tìm bội chung và bội chung nhỏ nhất của 4 và 6.
Giải
Ta có: B(4) = (0; 4; 8; 12; 16; 20; 24; 28;...}:
B(6) = (0; 12; 18; 24; 30;...}.
Các số 0; 12; 24;... vừa là bội của 4, vừa là bội của 6 nên BC(4, 6) = {0; 12; 24;...).
Số nhỏ nhất khác 0 trong tập hợp các bội chung của 4 và 6 là 12 nên BCNN(4, 6) = 12.

- X ∈ BC(a, b) nếu x⋮a, x⋮b.
- X ∈ BC(a, b, c) nếu x⋮a, x⋮b, x⋮c.
[trang 50]
Ví dụ 2
Trở lại tình huống mở đầu của bài, để mua cùng số lượng n cái mỗi loại thì n ∈ BC(4, 6). Để mua ít nhất thì n = BCNN(4, 6) = 12.
Vậy bạn Mai có thể mua ít nhất 12 cái mỗi loại hay mua 3 gói đĩa và 2 gói cốc.
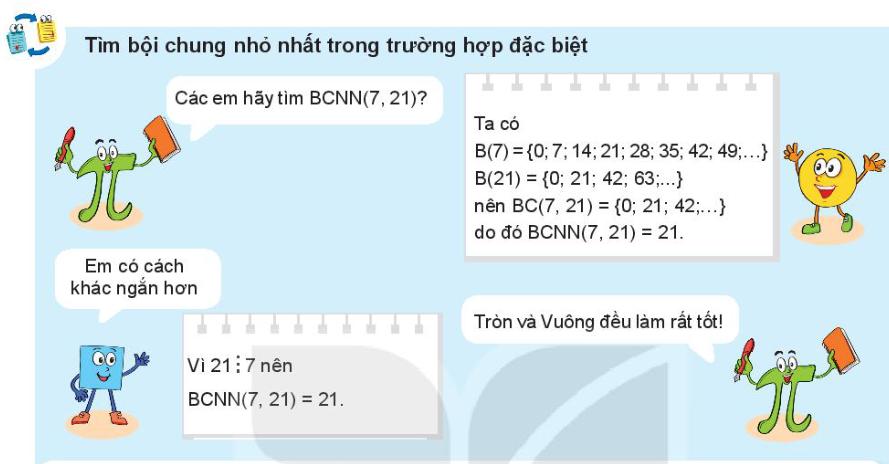
Tìm bội chung nhỏ nhất trong trường hợp đặc biệt
Các em hãy tìm BCNN(7,21)?
Ta có
B(7) = {0; 7; 14;21; 28; 35; 42; 49;...}
B(21) = {0; 21; 42; 63;..}
nên BC(7, 21) = (0; 21; 42;...} do đó BCNN(7, 21) = 21.
Em có cách khác ngắn hơn
Vì 21: 7 nên
BCNN(7, 21) = 21.
Tròn và Vuông đều làm rất tốt!
Nhận xét
• Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất đó
Nếu a⋮b thì BCNN(a, b) = a
• Mọi số tự nhiên đều là bội của 1. Do đó với mọi số tự nhiên a và b (khác 0), ta có:
BCNN(a, 1) = a; BCNN(a, b, 1) = BCNN(a, b).
❓ Tìm BCNN(36, 9).
Luyện tập 1
Tìm bội chung nhỏ nhất của:
a) 6 và 8;
b) 8; 9; 72.
Vận dụng
Có hai chiếc máy A và B. Lịch bảo dưỡng định kì đối với máy A là 6 tháng và đổi với máy B là 9 tháng. Hai máy vừa cùng được bảo dưỡng vào tháng 5. Hỏi sau ít nhất bao nhiêu tháng nữa thì hai máy lại được bảo dưỡng trong cùng một tháng?

Ta phân tích mỗi số ra thừa số nguyên tố để tìm các ước nguyên tố chung và riêng của các số đó.
2. CÁCH TÌM BỘI CHUNG NHỎ NHẤT
Ta có BCNN(4, 6) = 12 = 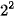 . 3, trong đó 2 và 3 là các ước nguyên tố chung và riêng của 4 và 6. Vậy có sự liên hệ gì giữa BCNN của các số và các ước nguyên tố chung và riêng của chúng? Chúng ta cùng tìm hiểu nhé.
. 3, trong đó 2 và 3 là các ước nguyên tố chung và riêng của 4 và 6. Vậy có sự liên hệ gì giữa BCNN của các số và các ước nguyên tố chung và riêng của chúng? Chúng ta cùng tìm hiểu nhé.
[trang 51]
Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố
Để tìm BCNN(75, 90) ta làm như sau:
1. Phân tích các số 75 và 90 ra thừa số nguyên tố, ta được:
75 = 3• 5• 5= 3• 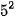 .
.
90 = 2• 3• 3• 5 = 2• 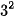 .5.
.5.
2. Ta thấy các thừa số chung là 3 và 5; thừa số riêng là 2.
3. Số mũ lớn nhất của 3 là 2, số mũ lớn nhất của 5 là 2, số mũ lớn nhất của 2 là 1.
Khi đó BCNN(75, 90) = 2 • 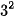 .
. 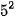 = 450
= 450
Các bước tìm BCNN của hai hay nhiều số lớn hơn 1:
1. Phân tích mỗi số ra thừa số nguyên tố;
2. Chọn ra các thừa số nguyên tố chung và riêng;
3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.
❓ Tìm bội chung nhỏ nhất của 9 và 15, biết: 9 = 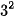 và 15 = 3- 5.
và 15 = 3- 5.
Ví dụ 3
Tìm BCNN( 18, 24, 40) bằng cách phân tích các số ra thừa số nguyên tố.
Giải
Phân tích các số 18; 24; 40 ra thừa số nguyên tố, ta được:
18 = 2. 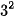 ;
;
24 =  . 3;
. 3;
40 =  . 5
. 5
Thừa số nguyên tố chung là 2 và riêng là 3 và 5.
Khi đó BCNN(18, 24, 40) =  •
• 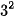 • 5 = 360.
• 5 = 360.

Ta thấy 18; 24; 40 có thừa số chung là 2 và các thừa số riêng là 3 và 5.
Tìm bội chung từ bội chung nhỏ nhất
Ta đã biết BC(4, 6) = (0; 12; 24;..}, BCNN(4, 6) = 12 và nhận thấy các số là bội chung của 4 và 6 đều là bội của 12.
Để tìm bội chung của các số đã cho ta có thể làm như sau:
1. Tim BCNN của các số.
2. Tìm các bội của BCNN đó.
❓ Biết bội chung nhỏ nhất của 8 và 6 là 24. Tìm các bội chung nhỏ hơn 100 của 8 và 6.
Ví dụ 4
Ta có BCNN( 18, 24, 40) = 360.
Từ đó, ta suy ra BC(18, 24, 40) = 10; 360; 720; 1 080);..) nên bội chung nhỏ hơn 900 của 18; 24 và 40 là 0; 360; 720.
[trang 52]
Luyện tập 2
Tìm bội chung nhỏ nhất của 15 và 54. Từ đó, hãy tìm các bội chung nhỏ hơn 1 000 của 15 và 54.
Thử thách nhỏ
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hói vào các thời điểm nào trong ngày (từ 10 giờ 35 phút đến 22 giờ) các xe buýt này lại xuất bên cùng một lúc?
| Bến xe Mỹ Đình | |
| Số xe | Thời gian |
| Xe 16 | 15 phút / chuyến |
| Xe 34 | 9 phút / chuyến |
| Xe 30 | 10 phút / chuyến |
3. QUY ĐỒNG MẪU CÁC PHÂN SỐ
Vận dụng BCNN để tìm mẫu chung của hai phân số
Để quy đồng mẫu hai phân số 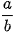 và
và 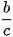 , ta phải tìm mẫu chung của hai phân số đó.
, ta phải tìm mẫu chung của hai phân số đó.
Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu.
Chẳng hạn, để quy đồng mẫu hai phân số 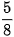 và
và 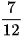 , ta làm như sau:
, ta làm như sau:
Ta có BCNN(8, 12) = 24, nên 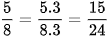 và
và 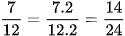
❓ Quy đồng mẫu hai phân số: 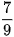 và
và 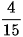
Ví dụ 5
Quy đồng mẫu các phân số sau: 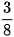 ,
, 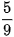 và
và 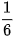
Giải
Ta có 6=2.3; 8= 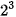 ; 9=
; 9= 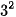 nên BCNN (6,8,9)=
nên BCNN (6,8,9)= 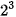 .
. 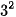 = 72
= 72
Ta có thể lấy mẫu chung của ba phân số trên là 72. Do đó
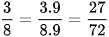 ;
; 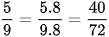 ;
; 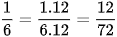
Ví dụ 6
Thực hiện phép tính:
a) 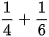 b)
b) 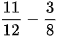
Giải
a) Ta có BCNN(4, 6) = 12 nên ta có thể lấy mẫu chung của hai phân số là 12 và:
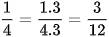
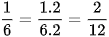
[trang 53]
Vậy 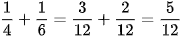
b) Ta có BCNN(8, 12) = 24 nên: 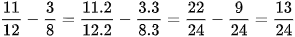
Luyện tập 3
1) Quy đồng mẫu các phân số sau:
a) 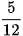 và
và 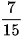 b)
b) 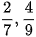 và
và 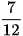
2) Thực hiện các phép tính sau:
a) 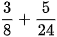 b)
b) 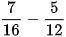
BÀI TẬP
2.36. Tìm bội chung nhỏ hơn 200 của:
a) 5 và 7;
b) 3, 4 và 10.
2.37. Tìm BCNN của:
a) 2• 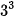 và 3• 5;
và 3• 5;
b) 2•5• 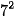 và 3•
và 3• 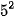 . 7.
. 7.
2.38. Tìm BCNN của các số sau:
a) 30 và 45;
b) 18, 27 và 45.
2.39. Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a: 28 và a: 32.
2.40. Học sinh lớp 6A khi xếp thành 3 hàng, 4 hàng hay 9 hàng đều vừa đủ. Biết sô học sinh của lớp từ 30 đến 40. Tính số học sinh lớp 6A.
2.41. Hai đội công nhân trồng được một số cây như nhau. Mỗi công nhân đội I đã trồng 8 cây, mỗi công nhân đội Il đã trồng 11 cây. Tính số cây mỗi đội đã trồng, biết rằng số cây đó trong khoảng từ 100 đến 200 cây.
2.42. Cứ 2 ngày, Hà đi dạo cùng bạn cún yêu quý của minh. Cứ 7 ngày, Hà lại tắm cho cún. Hôm nay, cún vừa được đi dạo, vừa được tắm. Hỏi sau ít nhất bao nhiêu ngày nữa thì cún vừa được. đi dạo, vừa được tắm?
2.43. Quy đồng mẫu các phân số sau:
a) 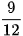 và
và 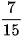 b)
b) 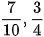 và
và 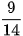
2.44. Thực hiện các phép tính sau:
a) 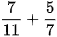 b)
b) 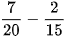
EM CÓ BIẾT?
LỊCH CAN CHI
Nhiều nước phương Đông trong đó có Việt Nam, gọi tên năm âm lịch bằng cách ghép 10 can theo thứ tự (Giáp, Ất, Bính, Đinh, Mậu, Kỉ, Canh, Tân, Nhâm, Quý) với 12 chi (Tí, Sửu, Dần, Mão, Thìn,Tị, Ngọ, Mùi, Thân, Dậu, Tuất, Hợi). Đầu tiên Giáp được ghép với Tí thành năm Giáp Tí. Cứ 10 năm Giáp lại được lặp lại; cứ 12 năm Tí lại được lặp lại:

Như vậy, cứ sau 60 năm (60 là BCNN của 10 và 12), năm Giáp Tí lại được lặp lại. Tên của các năm âm lịch khác cũng được lặp lại sau 60 năm.

























