Trang 123
A – TRẮC NGHIỆM
5.18. Cho dãy số (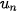
) với 
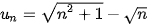. Mệnh đề đúng là
A.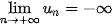 
.
B.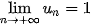 
C.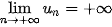 
.
D.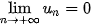 
5.19. Cho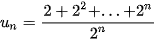 
. Giới hạn của dãy số (
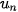) bằng
A. 1.
B. 2.
C.-1.
D. 0.
5.20. Cho cấp số nhân lùi vô hạn (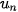) với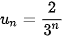 
. Tổng của cấp số nhân này bằng
A. 3.
B. 2.
C. 1.
D. 6.
5.21. Cho hàm số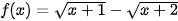 
. Mệnh đề đúng là
A.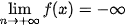 
.
B.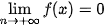 
.
C.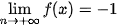 
.
D.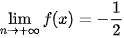 
.
5.22. Cho hàm số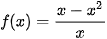 
. Khi đô 
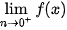bằng
A. 0.
B. 1.
C. +∞.
D. -1.
5.23. Cho hàm số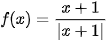 
. Hàm số f (x) liên tục trên
A. (-∞; +∞).
B. (-∞; -1]
C. (-∞; -1) ∪ (-1; +∞).
D. [-1; +∞).
5.24. Cho hàm số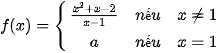 
. Hàm số f (x) liên tục tại x = 1 khi
A. a = 0.
B. a = 3.
C. a = 1.
D. a = 1.
Trang 124
B – TỰ LUẬN
5.25. Cho dãy số (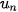
) có tính chất 
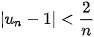. Có kết luận gì về giới hạn của dãy số này?
5.26. Tìm giới hạn của các dãy số sau:
a)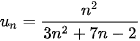 
;
b)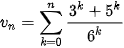 
;
c)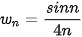 
5.27. Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số.
a) 1,(01);
b) 5,(132).
5.28. Tính các giới hạn sau:
a)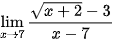 
;
b)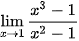 
;
c)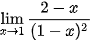 
;
d)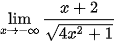 
.
5.29. Tính các giới hạn một bên:
a)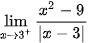 
;
b)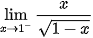 
.
5.30. Chứng minh rằng giới hạn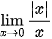 
không tồn tại.
5.31. Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho.
a)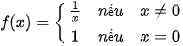 
tại điểm x = 0;
b)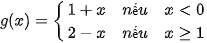 
tại điểm x = 1 .
5.32. Lực hấp dẫn tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm Trái Đất là
,
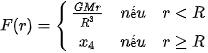trong đó M và R lần lượt là khối lượng và bán kính của Trái Đất, G là hằng số hấp dẫn. Xét tính liên tục của hàm số F (r).
5.33. Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng.
a)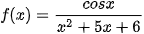 
;
b)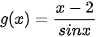 
.
5.34. Tìm các giá trị của a đề hàm số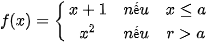 
liên tục trên R.
