Trang 31
| THUẬT NGỮ • Phương trình lượng giác • Phương trình lượng giác cơ bản • Công thức nghiệm | KIẾN THỨC, KĨ NĂNG • Nhận biết công thức nghiệm của phương trình lượng giác cơ bản bằng cách vận dụng đồ thị hàm số lượng giác tương ứng. • Tính nghiệm gần đúng của phương trình lượng giác cơ bản bằng máy tính cầm tay. • Giải phương trình lượng giác ở dạng vận dụng trực tiếp phương trình lượng giác cơ bản. • Giải quyết một số vấn đề thực tiễn gắn với phương trình lượng giác. |
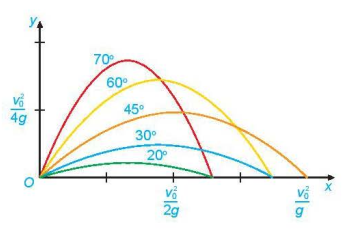
Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu có độ lớn 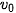 , không đổi. Tìm góc bắn ∝ để quả đạn pháo bay xa nhất, bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất.
, không đổi. Tìm góc bắn ∝ để quả đạn pháo bay xa nhất, bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất.

Hình 1.18. Dàn pháo
1. KHÁI NIỆM PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG
HĐ1. Nhận biết khái niệm hai phương trình tương đương
Cho hai phương trình 2x – 4 = 0 và (x - 2)(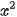 + 1) = 0
+ 1) = 0
Tìm và so sánh tập nghiệm của hai phương trình trên.
| Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm. Nếu phương trình f(x) = 0 tương đương với phương trình g(x) = 0 thì ta viết f(x) = 0 ⇔ g(x) = 0. |
Chú ý. Hai phương trình vô nghiệm là tương đương.
Ví dụ 1. Hai phương trình sau có tương đương không?
2x + 6 = 0 và 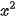 + 6x + 9 = 0.
+ 6x + 9 = 0.
Giải
Tập nghiệm của phương trình 2x + 6 =0 là 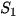 = {-3}.
= {-3}.
Phương trình 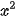 + 6x + 9 = 0 được viết lại thành
+ 6x + 9 = 0 được viết lại thành 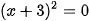 , do đó tập nghiệm của nó là
, do đó tập nghiệm của nó là 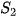 = {-3}.
= {-3}.
Vậy hai phương trình trên là tương đương.
Trang 32
Luyện tập 1. Xét sự tương đương của hai phương trình sau:
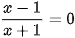 và
và 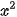 −1= 0.
−1= 0.
Chú ý. Để giải phương trình, thông thường ta biến đổi phương trình đó thành một phương trình tương đương đơn giản hơn. Các phép biến đổi như vậy gọi là các phép biến đổi tương đương.
Nếu thực hiện các phép biến đổi sau đây trên một phương trình mà không làm thay đổi điều kiện của nó thì ta được một phương trình mới tương đương với phương trình đã cho:
a) Cộng hay trừ hai vế với cùng một số hoặc một biểu thức:
f(x) = g(x) ⇔ f(x) + h(x) = g(x) + h(x).
b) Nhân hoặc chia hai về với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0:
f(x) = g(x) f(x)h(x) = g(x)h(x), (h(x)+0).
2.PHƯƠNG TRÌNH sinx = m
HĐ2. Nhận biết công thức nghiệm của phương trình sin x = 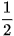
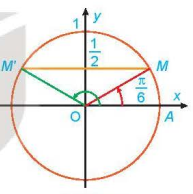
Hình 1.19
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.
Minh hoạ bằng đồ thị. Nghiệm của phương trình sin x = 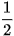 là hoành độ các giao điềm của đường thẳng y =
là hoành độ các giao điềm của đường thẳng y = 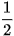 và đồ thị hàm số y = sin x.
và đồ thị hàm số y = sin x.
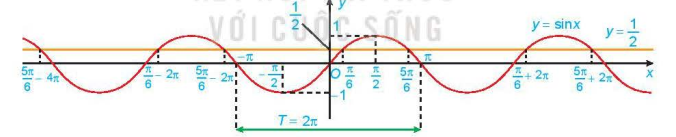
Hình 1.20. Đường thẳng y = 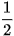 và đồ thị hàm số y = sin x
và đồ thị hàm số y = sin x
Tổng quát, xét phương trình sin x = m (*).
– Nếu |m| >1 thì phương trình (*) vô nghiệm vì |sin x| ≤ 1 với mọi x ∈ R.
– Nếu |m| ≤ 1 thì tồn tại duy nhất ∝ ∈ 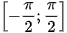 thoả mãn sin ∝ = m. Khi đó, trên đoạn có độ dài 2π là
thoả mãn sin ∝ = m. Khi đó, trên đoạn có độ dài 2π là 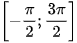 , phương trình (*) có các nghiệm ∝ và π – ∝ (H.1.21).
, phương trình (*) có các nghiệm ∝ và π – ∝ (H.1.21).
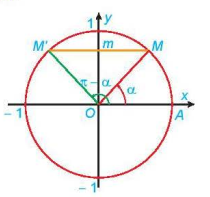
Hình 1.21
Trang 33
Do tính tuần hoàn với chu kì 2π của hàm sin, ta chỉ việc cộng vào các nghiệm này các bội nguyên của 2π thì sẽ được tất cả các nghiệm của phương trình (*).
| • Phương trình sin x = m có nghiệm khi và chỉ khi |m| ≤ 1. • Khi |m| ≤ 1, sẽ tồn tại duy nhất ∝ ∈ 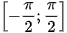 thoả mãn sin ∝ = m. Khi đó sin x = m ⇔ sin x = sin∝ ⇔ thoả mãn sin ∝ = m. Khi đó sin x = m ⇔ sin x = sin∝ ⇔ 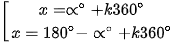 (k ∈ Z). (k ∈ Z). |
Chú ý
a) Nếu số đo của góc ∝ được cho bằng đơn vị độ thì
sin x = sin ∝° ⇔ 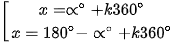 (k ∈ Z).
(k ∈ Z).
b) Một số trường hợp đặc biệt
• sin x = 0 ⇔ x = kπ, k ∈ Z.
• sin x = 1 ⇔ x =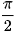 + k2π, k ∈ Z.
+ k2π, k ∈ Z.
• sin x =−1 ⇔ x = 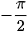 + k2π, k ∈ Z.
+ k2π, k ∈ Z.
Ví dụ 2. Giải các phương trình sau:
a) sin x = 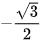
b) sin x = 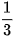
Giải
a) sin x = 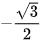 ⇔ sin x = sin
⇔ sin x = sin 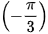 ⇔
⇔ 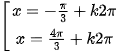 (k ∈ Z).
(k ∈ Z).
b) Gọi ∝ ∈ 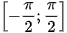 là góc thoả mãn sin∝ =
là góc thoả mãn sin∝ =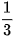 . Khi đó ta có:
. Khi đó ta có:
sin x = 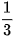 ⇔ sin x = sin∝ ⇔
⇔ sin x = sin∝ ⇔ 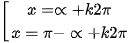 (k ∈ Z).
(k ∈ Z).

sinu = sinv ⇔ 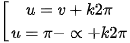 (k ∈ Z).
(k ∈ Z).
Ví dụ 3. Giải phương trình sin2x = sin(60° – 3x).
Giải
sin2x = sin(60° - 3x) ⇔ 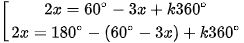
⇔ 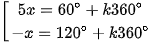 ⇔
⇔ 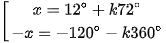 (k ∈ Z).
(k ∈ Z).
Trang 34
Ví dụ 4. Giải bài toán ở tình huống mở đầu.
Giải
Chọn hệ trục toạ độ có gốc toạ độ đặt tại vị trí khẩu pháo, trục Ox theo hướng khẩu pháo như hình bên. Khi đó, theo Vật lí, ta biết rằng vi quỹ đạo của quả đạn pháo có dạng đường parabol có phương trình (với g là gia tốc trọng trường) 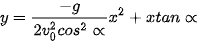 .
.
Cho y = 0 ta được 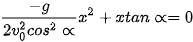 , suy ra x = 0 hoặc
, suy ra x = 0 hoặc 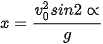 .
.
Quả đạn tiếp đất khi 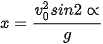 . Ta có
. Ta có 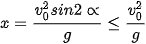 , dấu bằng xảy ra khi sin2∝ =1.
, dấu bằng xảy ra khi sin2∝ =1.
Giải phương trình sin2∝ =1, ta được ∝ = 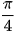 + kπ, k ∈ Z. Do 0 ≤ ∝ ≤
+ kπ, k ∈ Z. Do 0 ≤ ∝ ≤ 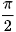 nên ∝ =
nên ∝ = 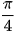 hay ∝ = 45°.
hay ∝ = 45°.
Vậy quả đạn pháo sẽ bay xa nhất khi góc bắn bằng 45°.
Luyện tập 2. Giải các phương trình sau:
a) sin x = 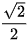
b) sin3x = -sin5x.
3. PHƯƠNG TRÌNH cos x= m
HĐ3. Nhận biết công thức nghiệm của phương trình 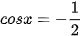
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng [-π; π).
b) Dựa vào tính tuần hoàn của hàm số côsin, hãy viết công thức nghiệm của phương trình đã cho.
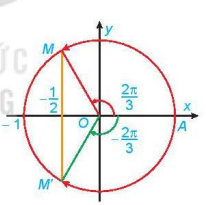
Hình 1.22a
Minh hoạ bằng đồ thị: Nghiệm của phương trình cos x = 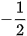 là hoành độ các giao điểm của đường thẳng y =
là hoành độ các giao điểm của đường thẳng y = 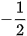 và đồ thị hàm số y = cos x.
và đồ thị hàm số y = cos x.

Hình 1.23. Đường thẳng y = 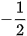 và đồ thị hàm số y = cos x
và đồ thị hàm số y = cos x
Trang 35
| • Phương trình cos x = m có nghiệm khi và chỉ khi |m| ≤ 1 cos x = m ⇔ cos x = cosα ⇔ |
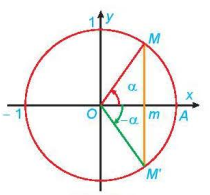
Hình 1.22b
Chú ý
a) Nếu số đo của góc a được cho bằng đơn vị độ thì
cos x ⇔ cos ∝° ⇔ 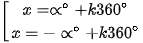 (k ∈ Z).
(k ∈ Z).
b) Một số trường hợp đặc biệt:
• cos x = 0 ⇔ x = 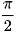 + kπ, k ∈ Z
+ kπ, k ∈ Z
• cos x =1 ⇔ x = k2π, k ∈ Z.
• cos x = -1 ⇔ x = π + k2π, k ∈ Z.
Ví dụ 5. Giải các phương trình sau:
a) cos x = 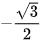
b) cos x = 0,1.
Giải
a) cos x = 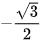 ⇔ cos x = cos
⇔ cos x = cos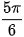 ⇔ x = ±
⇔ x = ±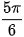 + k2π, k ∈ Z.
+ k2π, k ∈ Z.
b) Gọi ∝ ∈ [0; π] là góc thoả mãn cos∝ =0,1. Khi đó ta có:
cos x = 0,1 ⇔ cos x = cos∝ ⇔ x = ±∝ + k2π, k ∈ Z.

cosu = cosv ⇔ u = ±v + k2π (k ∈ Z).
Ví dụ 6. Giải phương trình cos2x = cos(45° − x).
Giải
cos2x = cos(45° - x) ⇔ 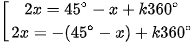
⇔ 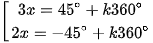 ⇔
⇔ 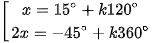 (k ∈ Z).
(k ∈ Z).
Luyện tập 3. Giải các phương trình sau:
a) 2cos x = -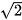 ;
;
b) cos3x – sin5x = 0.
Vận dụng
Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là ∝ (0° ≤ ∝ ≤ 360°) thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bởi công thức
F = 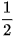 (1-cos∝).
(1-cos∝).
Trang 36
Xác định góc ∝ tương ứng với các pha sau của Mặt Trăng:
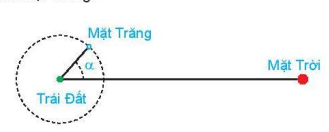
Trái Đất
Mặt Trăng
Mặt Trời
a) F = 0 (trăng mới);
b) F = 0,25 (trăng lưỡi liềm);
c) F = 0,5 (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng);
d) F = 1 (trăng tròn).
4. PHƯƠNG TRÌNH tan x = m
HĐ4. Nhận biết công thức nghiệm của phương trình tan x = 1
a) Quan sát Hình 1.24, hãy cho biết đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại mấy điểm trên khoảng 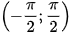 ?
?
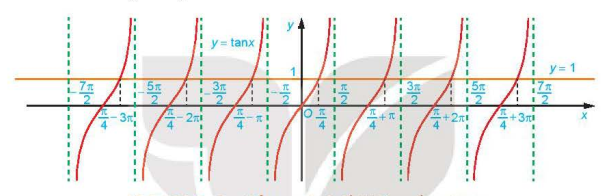
Hình 1.24. Đường thẳng y = 1 và đồ thị hàm số y = tan x
b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho.
| • Phương trình tan x = m có nghiệm với mọi m. tan x = m ⇔ tan x = tan∝ ⇔ x = ∝ + kπ (k ∈ Z). |
Chú ý. Nếu số đo của góc ∝ được cho bằng đơn vị độ thì tan x = tan∝° ⇔ x = ∝° + k180° (k ∈ Z).
Ví dụ 7. Giải các phương trình sau:
a) tanx = -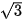 ;
;
b) tan x = 2.
Giải
a) tan x =- 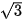 ⇔ tan x = tan
⇔ tan x = tan 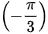 ⇔ x =
⇔ x = 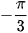 + kπ, k ∈ Z.
+ kπ, k ∈ Z.
b) Gọi α ∈ 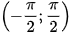 là góc thoả mãn tanα =2. Khi đó ta có:
là góc thoả mãn tanα =2. Khi đó ta có:
tan x = 2 ⇔ tan x = tanα ⇔ x = α + kπ, k ∈ Z.
Luyện tập 4. Giải các phương trình sau:
a) 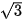 tan2x = −1;
tan2x = −1;
b) tan3x + tan5x = 0.
Trang 37
5. PHƯƠNG TRÌNH cot x = m
HĐ5. Nhận biết công thức nghiệm của phương trình cot x =-1
a) Quan sát Hình 1.25, hãy cho biết đường thẳng y = −1 cắt đồ thị hàm số y = cot x tại mấy điểm trên khoảng (0; π)?
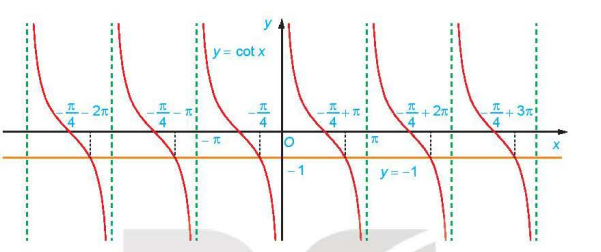
Hình 1.25. Đường thẳng y = −1 và đồ thị hàm số y = cot x
b) Dựa vào tính tuần hoàn của hàm côtang, hãy viết công thức nghiệm của phương trình đã cho.
| • Phương trình cot x = m có nghiệm với mọi m. • Với mọi m ∈ R, tồn tại duy nhất α ∈ (0; π) thoả mãn cotα = m. Khi đó cot x = m ⇔ cot x = cotα ⇔ x = α + kπ (k ∈ Z). |
Chú ý. Nếu số đo góc a được cho bằng đơn vị độ thì cot x=cotα° ⇔ x = α° + k180° (k ∈ Z).
Ví dụ 8. Giải các phương trình sau:
a) cot x =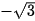 ;
;
b) cot x = 5.
Giải
a) cot x = 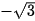 ⇔ cot x = cot
⇔ cot x = cot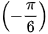 ⇔ x =
⇔ x = 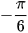 + kπ, k ∈ Z.
+ kπ, k ∈ Z.
b) Gọi ∝ ∈ (0; π) là góc thoả mãn cot∝ = 5. Khi đó ta có: cot x = 5 ⇔ cot x = cot∝ ⇔ x = ∝ + kπ, k ∈ Z.

cotu = cotv ⇔ u = v + kπ (k ∈ Z).
Luyện tập 5. Giải các phương trình sau:
a) cot x = 1;
b) 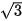 cot x + 1 = 0.
cot x + 1 = 0.
Trang 37
6. SỬ DỤNG MÁY TÍNH CẦM TAY TÌM MỘT GÓC KHI BIẾT GIÁ TRỊ LƯỢNG GIÁC CỦA NÓ
Các phím (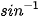 ), (
), (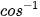 ) và (
) và (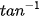 ) của máy tính cầm tay được dùng để tìm số đo (độ hoặc rađian) của một góc khi biết một trong các giá trị lượng giác của nó.
) của máy tính cầm tay được dùng để tìm số đo (độ hoặc rađian) của một góc khi biết một trong các giá trị lượng giác của nó.
| Để tìm số đo ta thực hiện các bước sau: Bước 1. Chọn đơn vị đo góc (độ hoặc rađian). Muốn tìm số đo độ (dòng trên cùng của màn hinh xuất hiện chữ nhỏ D), ta ấn  SHIFT MODE 3 Muốn tìm số đo rađian (dòng trên cùng của màn hình xuất hiện chữ nhỏ R), ta ấn  SHIFT MODE 4 Bước 2. Tìm số đo góc. Khi biết sin, côsin hay tang của góc ∝ cần tìm bằng m, ta lần lượt ấn các phím  SHIFT và một trong các phím SHIFT và một trong các phím  sin, cos và sin, cos và  tan, rồi nhập giá trị lượng giác m và cuối cùng ấn phím tan, rồi nhập giá trị lượng giác m và cuối cùng ấn phím  . Lúc này trên màn hình cho kết quả là số đo của góc ∝ (độ hoặc rađian). . Lúc này trên màn hình cho kết quả là số đo của góc ∝ (độ hoặc rađian). |
Chú ý
• Khi ở chế độ rađian, các phím (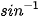 ), (
), (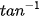 ), cho kết quả là một số thuộc khoảng
), cho kết quả là một số thuộc khoảng 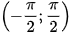 , phím (
, phím (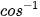 ) cho kết quả là một số thuộc khoảng (0; π), tất nhiên với (
) cho kết quả là một số thuộc khoảng (0; π), tất nhiên với (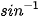 ) và (
) và (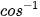 ) thì |m| ≤ 1.
) thì |m| ≤ 1.
• Khi ở chế độ số đo độ, các phím (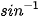 ) và (
) và (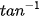 ) cho kết quả là số đo góc ∝ từ -90° đến 90°, phím (
) cho kết quả là số đo góc ∝ từ -90° đến 90°, phím (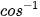 ) cho kết quả là số đo góc a từ 0° đến 180°, với (
) cho kết quả là số đo góc a từ 0° đến 180°, với (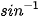 ) và
) và 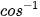 ) thì |m| ≤ 1.
) thì |m| ≤ 1.
• Khi có kết quả (trường hợp chọn đơn vị đo độ), ấn phím  thì đưa kết quả về dạng độ - phút - giây.
thì đưa kết quả về dạng độ - phút - giây.
Ví dụ 9. Sử dụng máy tinh cầm tay, tim số đo độ và rađian của góc α, biết sinα = 0,58.
Giải
Số đo độ:
| sinα | Bấm phím | Màn hình hiện | Kết quả của a (gần đúng) |
| 0,58 |  | 35.45054264 | 35°27'2" |
Số đo rađian:
| sinα | Bấm phím | Màn hình hiện | Kết quả của a (gần đúng) |
| 0,58 |  | 0.6187286907 | 0,61873 |
Luyện tập 6. Sử dụng máy tính cầm tay, tim số đo độ và rađian của góc ∝, biết:
a) cosα = -0,75;
b) tanα = 2,46;
c) cotα = -6,18.
Trang 39
BÀI TẬP
1.20. Giải các phương trình sau:
a) sin x = 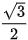 ;
;
b) 2cos x = 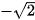 ;
;
c) 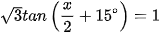 ;
;
d) cot(2x - 1) = cot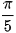 .
.
1.21. Giải các phương trình sau:
a) sin2x + cos4x = 0;
b) cos3x = -cos7x.
1.22. Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu 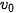 = 500 m/s hợp với phương ngang một góc ∝. Trong Vật lí, ta biết rằng, nếu bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất thì quỹ đạo của quả đạn tuân theo phương trình
= 500 m/s hợp với phương ngang một góc ∝. Trong Vật lí, ta biết rằng, nếu bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất thì quỹ đạo của quả đạn tuân theo phương trình 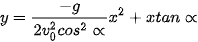 , ở đó g = 9,8 m/s
, ở đó g = 9,8 m/s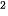 là gia tốc trọng trường.
là gia tốc trọng trường.
a) Tính theo góc bắn ∝ tầm xa mà quả đạn đạt tới (tức là khoảng cách từ vị trí bắn đến điểm quả đạn chạm đất).
b) Tìm góc bắn ∝ đề quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m.
c) Tìm góc bắn ∝ để quả đạn đạt độ cao lớn nhất.
1.23. Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình
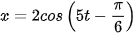
Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimét. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
| Em có biết? Lượng giác được phát triển bởi các nhà thiên văn học người Hy Lạp cổ đại, nhữngngười coi bầu trời là nằm bên trong của một mặt cầu, do đó lẽ tự nhiên là các hình tam giác trên mặt cầu được nghiên cứu khá sớm bởi Menelaus ở Alexandria vào khoảng năm 100 sau Công nguyên và các hình tam giác trên mặt phẳng được nghiên cứu muộn hơn nhiều. Cuốn sách đầu tiên chứa đựng các phương pháp xử lí có hệ thống về lượng giác phẳng và lượng giác cầu được viết bởi nhà thiên văn học người Ba Tư Nasir Eddin, khoảng năm 1250 sau Công nguyên. Regiomontanus (1436 – 1476) là người có công lớn trong việc chuyển Lượng giác từ Thiên văn học sang Toán học. Công trình của ông đã được cải tiến bởi Copernicus (1473 – 1543) và một học trò của Copernicus là Rhaeticus (1514 – 1576). Cuốn sách của Rhaeticus là cuốn sách đầu tiên định nghĩa các hàm lượng giác là tỉ số các cạnh của tam giác, mặc dù ông chưa đưa ra tên gọi như hiện nay của chúng. Các tên gọi và kí hiệu như ngày nay chúng ta dùng được đưa ra bởi Leonhard Euler (1707 – 1783), người đã xây dựng lí thuyết hiện đại về các hàm số lượng giác trong cuốn “Mở đầu về giải tích các đại lượng vô cùng bé" xuất bản năm 1748. Lượng giác là ngành khoa học có nhiều ứng dụng. Có thể kể đến việc sử dụng Lượng giác trong các vấn đề đo đạc của Thiên văn và Địa lí, cũng như những ứng dụng phong phú của Lượng giác trong Lí thuyết số, Cơ học, Điện học, Hoá học, Sinh học, Hải dương học, Đỗ hoạ máy tính, Lí thuyết âm nhạc và nhiều lĩnh vực khác. (Theo C.B. Boyer, U.C. Merzbach, A History of Mathematics, Third Edition, Wiley, 2011). |
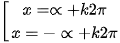 (k ∈ Z).
(k ∈ Z).
























