Trang 17
| THUẬT NGỮ • Công thức cộng • Công thức nhân đối • Công thức biến đổi tích thành tổng • Công thức biến đổi tổng thành tích | KIẾN THỨC, KĨ NĂNG • Mô tả các phép biến đổi lượng giác cơ bản: công thức cộng; công thức góc nhân đôi; công thức biến đổi tích thành tổng; công thức biến đổi tổng thành tích. • Giải quyết một số vấn đề thực tiễn gắn với giá trị lượng giác của góc lượng giác và các phép biến đổi lượng giác. |
Một thiết bị trễ kĩ thuật số lặp lại tín hiệu đầu vào bằng cách lặp lại tín hiệu đó trong một khoảng thời gian cố định sau khi nhận được tín hiệu. Nếu một thiết bị như vậy nhận được nốt thuần 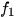 (t)=5sint và phát lại được nốt thuần
(t)=5sint và phát lại được nốt thuần 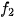 (t) = 5cost thì âm kết hợp là f(t) =
(t) = 5cost thì âm kết hợp là f(t) = 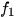 (t) +
(t) + 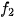 (t), trong đó t là biến thời gian. Chứng tỏ rằng âm kết hợp viết được dưới dạng f(t) = ksin(t + φ), tức là âm kết hợp là một sóng âm hình sin. Hãy xác định biên độ âm k và pha ban đầu φ (-π ≤ φ ≤ π) của sóng âm.
(t), trong đó t là biến thời gian. Chứng tỏ rằng âm kết hợp viết được dưới dạng f(t) = ksin(t + φ), tức là âm kết hợp là một sóng âm hình sin. Hãy xác định biên độ âm k và pha ban đầu φ (-π ≤ φ ≤ π) của sóng âm.
1. CÔNG THỨC CỘNG
HĐ1. Nhận biết công thức cộng
a) Cho a = 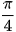 và b =
và b = 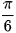 , hãy chứng tỏ cos(a – b) = cosacosb + sinasinb.
, hãy chứng tỏ cos(a – b) = cosacosb + sinasinb.
b) Bằng cách viết a + b = a − (−b) và từ công thức ở HĐ1a, hãy tính cos(a+b).
c) Bằng cách viết sin (a − b) = cos 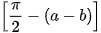 = cos
= cos 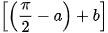 và sử dụng công thức vừa thiết lập ở HĐ1b, hãy tính sin(a - b)
và sử dụng công thức vừa thiết lập ở HĐ1b, hãy tính sin(a - b)
| cos(a - b) = cosacosb + sinasinb cos(a+b)= cosacosb - sinasinb sin(a - b) = sinacosb - cosasinb sin(a+b) = sinacosb + cosasinb tan(a-b) = 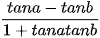 tan(a+b) = 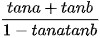 (giả thiết các biểu thức đều có nghĩa). |
Ví dụ 1. Không dùng máy tính, hãy tính:
a) cos75°:
b) tan 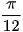
Trang 18
Giải
a) cos75° = cos(45° + 30°) = cos 45°cos 30° - sin 45°sin 30° = 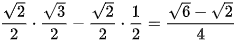 .
.
b) 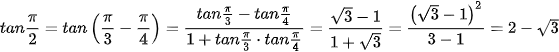 .
.
Ví dụ 2. Chứng minh rằng 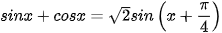 .
.
Giải
Ta có
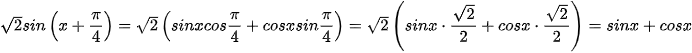 .
.
Đẳng thức được chứng minh.
Luyện tập 1. Chứng minh rằng:
a) 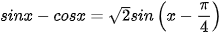
b) 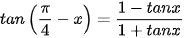
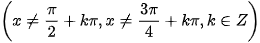 .
.
Vận dụng 1. Giải bài toán trong tình huống mở đầu.
2. CÔNG THỨC NHÂN ĐÔI
HD2. Xây dựng công thức nhân đôi
Lấy b = a trong các công thức cộng, hãy tìm công thức tính: sin2a, cos2a; tan2a.
sin2a = 2sinacosa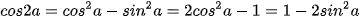 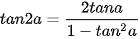 |
Ví dụ 3. Cho cos a = 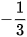
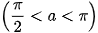 . Tính sin2a.
. Tính sin2a.
Giải
Vì 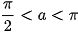 nên sina > 0. Do đó
nên sina > 0. Do đó 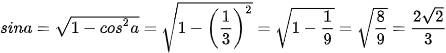 .
.
Vậy sin2a = 2sinacosa = 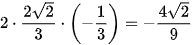 .
.
Trang 19
Luyện tập 2. Không dùng máy tính, tính cos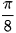

Công thức hạ bậc:
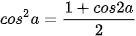
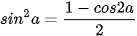 .
.
3. CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG
HĐ3. Xây dựng công thức biến đổi tích thành tổng
a) Từ các công thức cộng cos(a + b) và cos(a – b), hãy tìm: cosacosb; sinasinb.
b) Từ các công thức cộng sin(a + b) và sin(a – b), hãy tìm: sinacosb.
cosacosb = 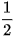 [cos(a - b) + cos(a + b)] [cos(a - b) + cos(a + b)]sinasinb = 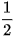 cos(a - b)-cos (a + b)] cos(a - b)-cos (a + b)]sinacosb = 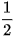 [sin(a - b) + sin(a + b)]. [sin(a - b) + sin(a + b)]. |
Ví dụ 4. Tính giá trị của các biểu thức:
Giải
Ta có:
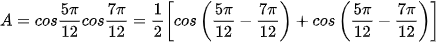
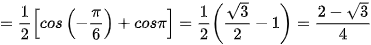 .
.
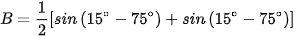
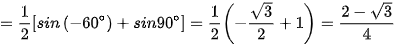 .
.
Luyện tập 3. Không dùng máy tính, tính giá trị của các biểu thức:
A = cos 75°cos15°;
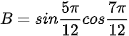 .
.
4. CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH
HĐ4. Xây dựng công thức biến đổi tổng thành tích
Trong các công thức biến đổi tích thành tầng ở Mục 3, đặt u = a – b, v = a + b và viết các công thức nhận được.
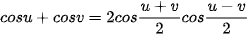
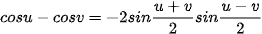
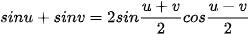
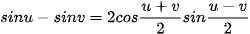
Ví dụ 5. Không dùng máy tính, tính giá trị của biểu thức 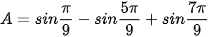 .
.
Giải
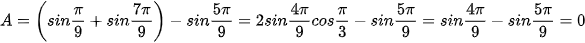 .
.
Luyện tập 4. Không dùng máy tính, tính giá trị của biểu thức
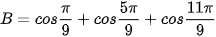 .
.
Vận dụng 2. Khi nhấn một phím trên điện thoại cảm ứng, bàn phím sẽ tạo ra hai âm thuần, kết hợp với nhau để tạo ra âm thanh dạng duy nhất phím. Hình 1.13 cho thấy tần số thấp 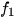 và tần số cao
và tần số cao 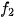 liên quan đến mỗi phím. Nhấn một phím sẽ tạo ra sóng âm y = sin(2π
liên quan đến mỗi phím. Nhấn một phím sẽ tạo ra sóng âm y = sin(2π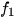 t) + sin(2π
t) + sin(2π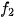 t), ở đó t là biến thời gian (tính bằng giây).
t), ở đó t là biến thời gian (tính bằng giây).
a) Tìm hàm số mô hình hoa âm thanh được tạo ra khi nhấn phím 4.
b) Biến đổi công thức vừa tìm được ở câu a về dạng tích của một hàm số sin và một hàm số côsin.
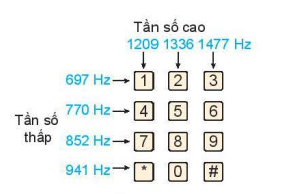
Tần số cao: 1209, 1336, 1477, Hz
Tần số thấp: 697 Hz, 770 Hz, 882Hz, 941Hz
Hình 1.13
Trang 21
BÀI TẬP
1.7. Sử dụng 15° = 45° – 30°, hãy tính các giá trị lượng giác của góc 15°.
1.8. Tính:
a) 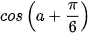 , biết
, biết 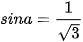 và
và 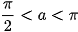 ;
;
b) 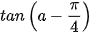 , biết
, biết 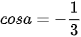 và
và 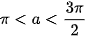 .
.
1.9. Tính sin2a, cos2a, tan2a, biết:
a) sina = 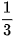 và
và 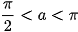 ;
;
b) sina + cosa = 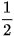 và
và 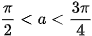 .
.
1.10. Tính giá trị của các biểu thức sau:
a) 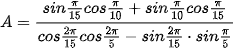 ;
;
b) 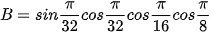 .
.
1.11. Chứng minh đẳng thức sau:
sin(a + b) sin(a - b) = 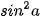 -
- 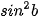 =
= 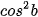 -
- 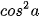 .
.
1.12. Cho tam giác ABC có 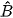 = 75°;
= 75°; 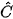 = 45° và a = BC = 12 cm.
= 45° và a = BC = 12 cm.
a) Sử dụng công thức S = 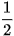 absinC và định lí sin, hãy chứng minh diện tích của tam giác ABC cho bởi công thức
absinC và định lí sin, hãy chứng minh diện tích của tam giác ABC cho bởi công thức
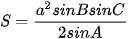
b) Sử dụng kết quả ở câu a và công thức biến đổi tích thành tổng, hãy tính diện tích S của tam giác ABC.
1.13. Trong Vật lí, phương trình tổng quát của một vật dao động điều hoà cho bởi công thức x(t)= Acos(ωt + φ), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời
điểm t, A là biên độ dao động (A > 0) và φ ∈ [-π; π] là pha ban đầu của dao động.
Xét hai dao động điều hoà có phương trình:
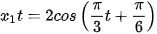 (cm),
(cm),
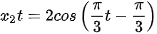 (cm).
(cm).
Tìm dao động tổng hợp x(t)= 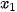 (t) +
(t) + 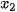 (t) và sử dụng công thức biến đổi tổng thành tích để tìm biên độ và pha ban đầu của dao động tổng hợp này.
(t) và sử dụng công thức biến đổi tổng thành tích để tìm biên độ và pha ban đầu của dao động tổng hợp này.

























