(Trang 91)
Ví dụ 1
Cho các điểm A, B, C, D, E như Hình 9.26, biết rằng AB = 6 cm, AC = 9 cm, AD = 8 cm, BC = 12 cm, BD = 4 cm. Chứng minh rằng △ABC ᔕ △BDA và △BDE ᔕ △ACE.
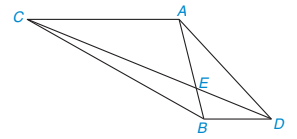
Hình 9.26
Hai tam giác ABC và BDA có: 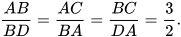
Vậy △ABC ᔕ △BDA (c.c.c). Từ đó suy ra 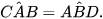
Do đó, AC // BD (có hai góc so le trong bằng nhau).
Vậy đường thẳng AC song song với cạnh BD của tam giác BDE và cắt hai cạnh BE, DE kéo dài lần lượt tại A và C. Suy ra △BDE ᔕ △ACE.
Ví dụ 2
Cho góc xOy, các điểm A, B nằm trên tia Ox và các điểm C, D nằm trên tia Oy như Hình 9.27, sao cho OA = 2 cm, OB = 6 cm, OC = 3 cm, OD = 4 cm. Biết AD cắt BC tại điểm E. Hãy tính tỉ số 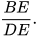
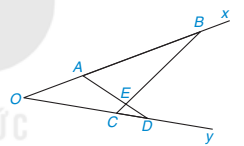
Hình 9.27
Giải
| GT | Góc xOy; A, B ∈ Ox; C, D ∈ Oy; OA = 2 cm, OB = 6 cm, OC = 3 cm, OD = 4 cm; AD cắt BC tại E. |
| KL | Tính 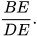 |
Hai tam giác OAD và OCB có: Ô chung, 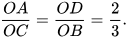
Vậy △OAD ᔕ △OCB (c.g.c). Suy ra 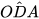 =
= 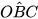 (*).
(*).
Hai tam giác AEB và CED có:
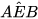 =
= 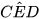 (hai góc đối đỉnh),
(hai góc đối đỉnh), 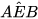 =
= 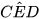 (theo (*)).
(theo (*)).
Vậy △AEB ᔕ △CED (g.g). Do đó 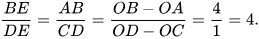
(Trang 92)
BÀI TẬP
9.11. Cho △ABC ᔕ △DEF. Biết Â= 60°, Ê =80°, hãy tính số đo các góc 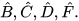 .
.
9.12. Cho △ABC ᔕ △A'B'C'. Biết AB = 3 cm, A'B' = 6 cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'.
9.13. Cho hình thang ABCD (AB // CD) có 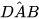 =
= 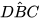 (H.9.28).
(H.9.28).
a) Chứng minh rằng △ABD ᔕ △BDC.
b) Giả sử AB = 2 cm, AD = 3 cm, BD = 4 cm. Tính độ dài các cạnh BC và DC.
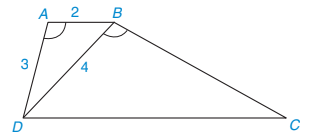
Hình 9.28
9.14. Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE II AB, EF II BC, DE = 4 cm, AB = 6 cm. Chứng minh rằng △AEF ᔕ △ECD và tính tỉ số đồng dạng.
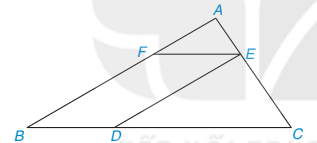
Hình 9.29
9.15. Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng 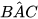 =
= 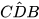 . Chứng minh rằng △AED ᔕ △BEC.
. Chứng minh rằng △AED ᔕ △BEC.
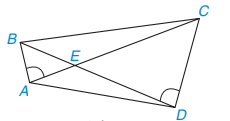
Hình 9.30
9.16. Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM = MD, 2BN = NC. Biết AB = 5 cm, CD = 6 cm. Hãy tính độ dài đoạn thẳng MN.