(Trang 74)
Ví dụ
Cho điểm M thuộc đoạn AB và hai điểm C, D như hình 4.43 sao cho ∠BAC = ∠BAD, ∠ABC = ∠ABD. Chứng minh rằng:
a)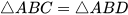 
; b) 
.
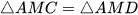Giải
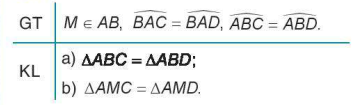
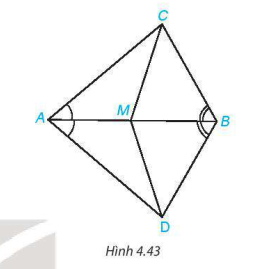
a) Hai tam giác ABC và ABD có:
∠BAC = ∠BAD (theo giả thiết);
AB là cạnh chung;
∠ABC = ∠ABD (theo giả thiết).
Vậy 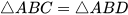(g.c.g).
b) Hai tam giác AMC và AMD có:
AM là cạnh chung;
∠MAC = ∠BAC = ∠BAD = MAD (theo giả thiết);
AC = AD (vì ).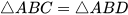
Vậy 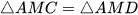(c.g.c).
BÀI TẬP
4.16. Cho hai tam giác ABC và DEF thoả mãn AB = DE, AC = DF, ∠BAC = ∠EDF = 60°, BC = 6cm, ∠ABC = 45°. Tính độ dài EF và số đo các góc ACB, DEF, EFD.
4.17. Cho hai tam giác ABC và DEF thoả mãn AB = DE, ∠ABC = ∠DEF = 70°, ∠BAC = ∠EDF = 60°, AC = 6cm.
Tính độ dài cạnh DF.
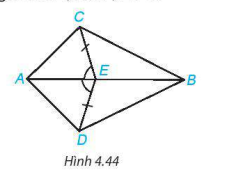
4.18. Cho hình 4.44, biết EC = ED và ∠AEC = ∠AED. Chứng minh rằng:
a)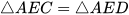 
; b)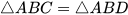 
.
4.19. Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho ∠CAO = ∠CBO.
a) Chứng minh rằng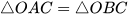 
.
b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng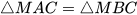 
.
