(Trang 63)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
|
|
Ta nói hai đoạn thẳng bằng nhau nếu chúng có cùng độ dài, hai góc bằng nhau nếu chúng có cùng số đo góc. Vậy hai giác giác như thế nào thì được gọi là bằng nhau và làm thế nào để kiểm tra được hai tam giác đó bằng nhau? Trong bài này chúng ta sẽ trả lời câu hỏi đó.
1) HAI TAM GIÁC BẰNG NHAU
Hai tam giác bằng nhau
HĐ1 Gấp đôi một tờ giấy rồi cắt như hình 4.9.
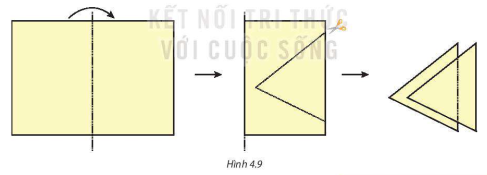
Phần được cắt ra là hai tam giác "chồng khít" lên nhau. Theo em:
- Cạnh tương ứng có bằng nhau không?
- Các góc tương ứng có bằng nhau không?

(Trang 64)
Hai tam giác ABC và A'B'C' (H.4.10) bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, nghĩa là:
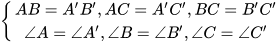
Khi đó ta viết 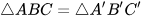 .
.
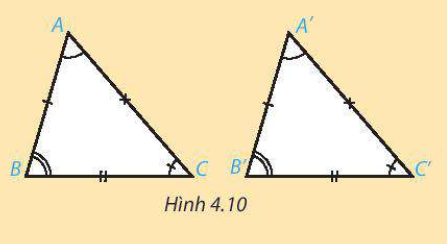
Ở đây hai đỉnh A và A' (B và B', C và C') là hai đỉnh tương ứng; hai góc A và A' (B và B', C và C') là hai góc tương ứng; hai cạnh AB và A'B' (AC và A'C', BC và B'C') là hai cạnh tương ứng.
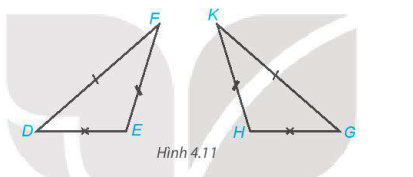
Biết hai tam giác trong hình 4.11 bằng nhau, em hãy chỉ ra các cặp cạnh tương ứng, các cặp góc tương ứng và viết đúng kí hiệu bằng nhau của cặp tam giác đó.
Ví dụ 1
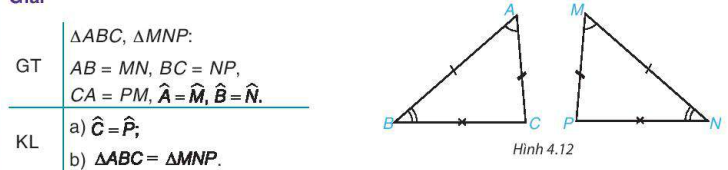
Cho tam giác ABC và MNP có AB = MN, BC = NP, CA = PM, ∠A = ∠M, ∠B = ∠N.
Chứng minh rằng
a) ∠C = ∠P;
b)  .
.
Giải
a) Trong tam giác ABC ta có ∠A + ∠B + ∠C = 180°, suy ra ∠C = 180° - ∠A - ∠B. (1)
Trong tam giác MNP ta có ∠M + ∠N + ∠P = 180°, suy ra ∠P = 180° - ∠M - ∠N. (2)
Vì ∠A = ∠M , ∠B = ∠N nên từ (1) và (2) ta có ∠C = ∠P.
(Trang 65)
b) Hai tam giác ABC và MNP có:
AB = MN, BC =NP, CA = PM (theo giả thiết);
∠A = ∠M, ∠B = ∠N (theo giả thiết), ∠C = ∠P (chứng minh trên).
Vậy hai tam giác ABC và MNP có các cạnh và các góc tương ứng bằng nhau.
Do đó 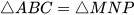 .
.
Luyện tập 1
Cho tam giác ABC bằng tam giác DEF (H.4.13). Biết rằng BC = 4cm, ∠ABC = 40°, ∠ACB = 60°. Hãy tính độ dài đoạn thẳng EF và số đo góc EDF.
2) TRƯỜNG HỢPP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC: CẠNH - CẠNH - CẠNH (C.C.C)
Để kiểm tra hai tam giác bằng nhau có nhất thiết phải kiểm tra cả ba cạnh tương ứng và ba góc tương ứng bằng nhau hay không?
Trường hợp bằng nhau cạnh - cạnh - cạnh
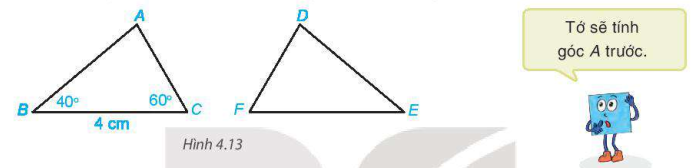
HĐ2 Vẽ tam giác ABC có AB = 5cm, AC = 4cm, BC = 6cm theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng BC = 6cm.
- Vẽ cung tròn tâm B bán kính 5cm và cung tròn tâm C bán kính 4cm sao cho hai cung tròn cắt nhau tại điểm A (H.4.14).
- Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.

(Trang 66)
HĐ3 Tương tự, vẽ thêm tam giác A'B'C' có A'B' = 5cm, A'C' = 4cm, B'C' = 6cm.
- Dùng thước đo góc kiểm tra xem các góc tương ứng của hai tam giác ABC và A'B'C' có bằng nhau không.
- Hai tam giác ABC và A'B'C' có bằng nhau không?
Ta thừa nhận định lí sau:
Trường hợp bằng nhau cạnh - cạnh - cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
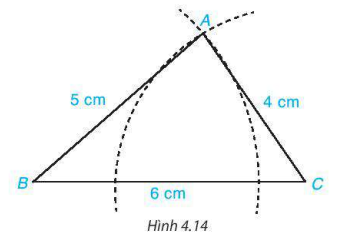
Trong hình 4.15, những cặp tam giác nào bằng nhau?
Ví dụ 2
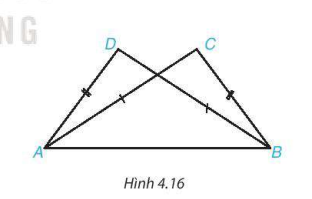
Cho hình 4.16, biết AC = BD, AD = BC.
Chứng minh rằng 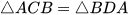 .
.
Giải
Hai tam giác ACB và BDA có:
AC = BD (theo giả thiết);
BC = AD (theo giả thiết);
AB là cạnh chung.
Vậy 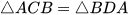 (c.c.c).
(c.c.c).
Luyện tập 2
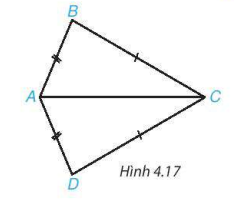
Cho hình 4.17, biết AB = AD, BC = DC. Chứng minh rằng 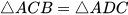 .
.
(Trang 67)
Vận dụng Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy như sau:
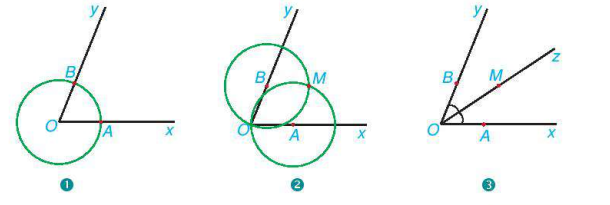
- Vẽ đường tròn tâm O cắt Ox, Oy lần lượt tại A và B.
- Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.
- Vẽ tia Oz đi qua M.
Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
BÀI TẬP
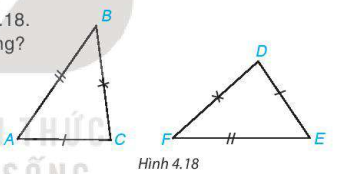
4.4. Cho tam giác ABC và DEF như hình 4.18. Trong các khẳng định sau, khẳng định nào đúng?
(1)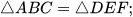
(2)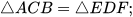
(3)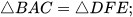
(4)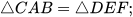
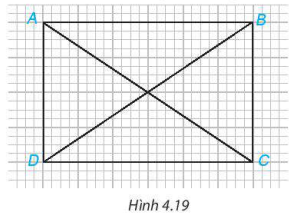
4.5. Trong hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.
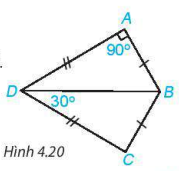
4.6. Cho hình 4.20, biết AB = CB, AD = CD, ∠DAB = 90°, ∠BDC = 30°.
a) Chứng minh rằng 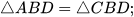
b) Tính ∠ABC.