(Trang 70)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
|
|
Trong thực tế , nhiều khi ta không thể đo được hết các cạnh của hai tam giác để khẳng định được chúng có bằng nhau hay không. Khi đó, có cách nào khác giúp ta biết được điều đó?
1) TRƯỜNG HỢP BẰNG NHAU THỨ HAI CỦA TAM GIÁC: CẠNH - GÓC - CẠNH (C.G.C)
Trường hợp bằng nhau cạnh - góc - cạnh
HĐ1 Vẽ ∠xAy = 60°. Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4cm, AC = 3cm.
Nối điểm B với điểm C ta được tam giác ABC (H.4.27).
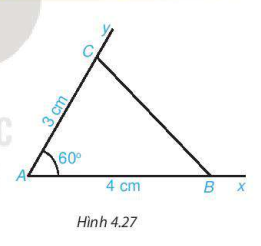
Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.
HĐ2 Vẽ thêm tam giác A'B'C' với ∠B'A'C' = 60°, A'B' = 4cm và A'C' = 3cm (H.4.28).
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và A'B'C'.
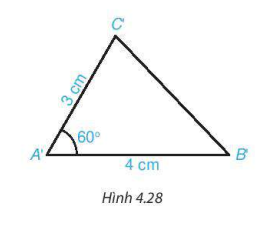
- Hai tam giác ABC và A'B'C' có bằng nhau không?
- Độ dài cạnh BC và B'C' của hai tam giác em vừa vẽ có bằng các cạnh BC và B'C' của hai tam giác các bạn khác vẽ không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
(Trang 71)
Trong tam giác ABC (H.4.27), góc BAC (hay đơn giản là góc A) được gọi là góc xen giữa hai cạnh AB và AC của tam giác ABC.
Ta thừa nhận định lí sau:
Trường hợp bằng nhau cạnh - góc - cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
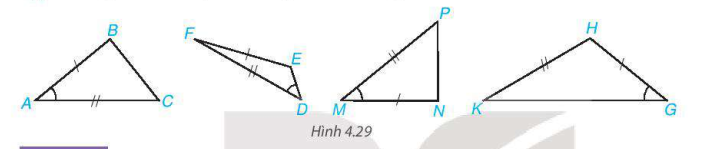
Trong Hình 4.29, hai tam giác nào bằng nhau?
Ví dụ 1
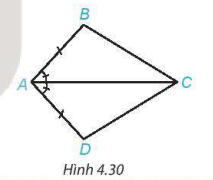
Xét hai tam giác ABC và ADC như hình 4.30. Ta có:
AB = AD;
∠BAC = ∠DAC;
AC là cạnh chung.
Vậy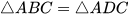 
(c.g.c).
Luyện tập 1
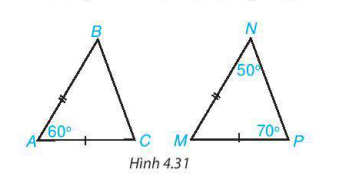
Hai tam giác ABC và MNP trong hình 4.31 có bằng nhau không? Vì sao?
Vận dụng
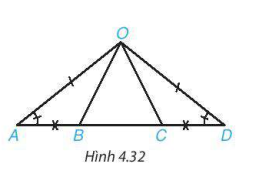
Cho hình 4.32, biết ∠OAB = ∠ODC, OA = OD và AB = CD.
Chứng minh rằng:
a) AC = DB;
b)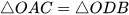 
.
(Trang 72)
2) TRƯỜNG HỢP BẰNG NHAU THỨ BA CỦA TAM GIÁC: GÓC - CẠNH - GÓC (G.C.G)
Trường hợp bằng nhau góc - cạnh - góc
HĐ3 Vẽ đoạn thẳng BC = 3cm. Vẽ hai tia Bx và Cy sao cho ∠xBC = 80°, ∠yCB = 40° như hình 4.33.
Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33).
Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC.
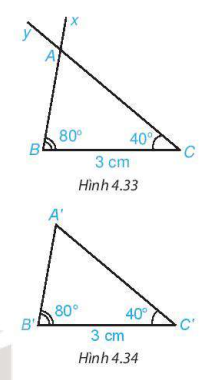
HĐ4 Vẽ thêm tam giác A'B'C' sao cho B'C' = 3cm, ∠A'B'C' = 80°, ∠A'C'B' = 40° (H.4.34).
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác ABC và A'B'C'.
Hai tam giác ABC và A'B'C' có bằng nhau không?
Trong tam giác ABC (H.4.33), hai góc ∠ABC, ∠ACB (gọi đơn giản là góc B và góc C) được gọi là các góc kề cạnh BC của tam giác ABC. Ta thừa nhận định lí sau:
Trường hợp bằng nhau góc - cạnh - góc (g.c.g)
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
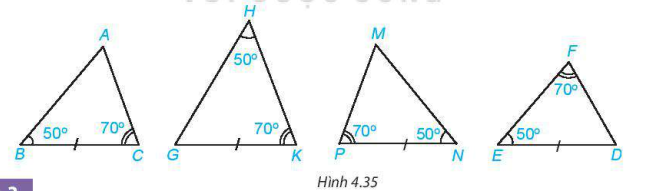
Hai tam giác nào trong hình 4.35 bằng nhau?
Ví dụ 2
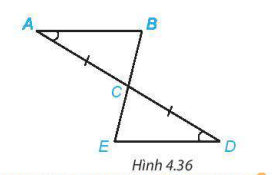
Xét hai tam giác ABC và DEC như hình 4.36. Ta có:
∠BAC = ∠EDC (theo giả thiết);
AC = DC (theo giả thiết);
∠BCA = ∠ECD (hai góc đối đỉnh).
Vậy 
(g.c.g).
(Trang 73)
Luyện tập 2
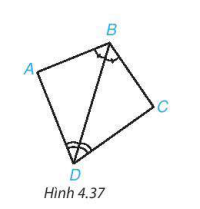
Chứng minh hai tam giác ABD và CBD trong hình 4.37 bằng nhau.
Thử thách nhỏ
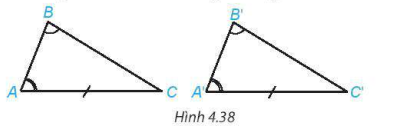
Bạn Lan nói rằng: "Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau" (H.4.38).
Theo em bạn Lan nói có đúng không? Vì sao?
BÀI TẬP
4.12. Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
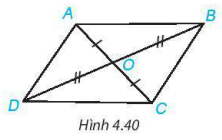
4.13. Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như hình 4.40.
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;
b) Chứng minh rằng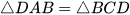 
.
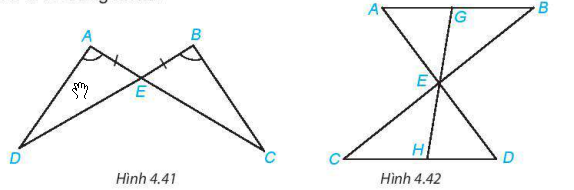
4.14. Chứng minh rằng hai tam giác ADE và BCE trong hình 4.41 bằng nhau.
4.15. Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:
a)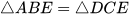 
; b) EG = EH.
