Bài 8: Mẫu số liệu ghép nhóm: Trong kì thi tốt nghiệp Trung học phổ thông năm 2021 đợt 1 có 344 752 thí sinh dự thi cả ba môn Toán, Vật lí, Hóa học (theo: vietnamnet.vn, ngày 26/07/2021). Giả sử điểm thi của các thí sinh này được cho trong bảng số liệu sau:
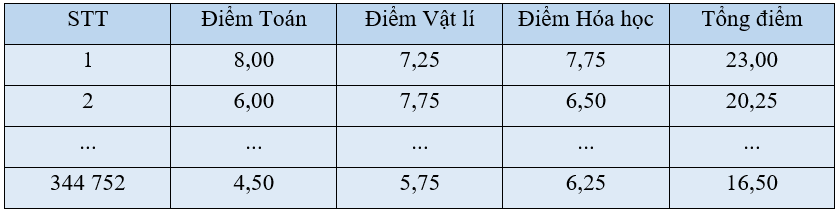
Các trường đại học, cao đẳng tuyển sinh theo tổ hợp A00 quan tâm đến tổng điểm ba môn của các thí sinh này. Biểu diễn dãy số liệu về tổng điểm ba môn của các thí sinh này thế nào để các trường thấy được bức tranh tổng thể về kết quả thi?
Lời giải:
Để thuận tiện cho các trường thấy được bức tranh tổng thể về kết quả thi, ta nên biểu diễn dãy số liệu về tổng điểm ba môn của các thí sinh theo mẫu số liệu ghép nhóm với các nhóm phù hợp.
1. Giới thiệu về mẫu số liệu ghép nhóm
HĐ1 trang 59 Toán 11 Tập 1: Xét dữ liệu cho trong tình huống mở đầu.
a) Mẫu số liệu về tổng điểm, kí hiệu là (T), có bao nhiêu giá trị?
b) Nếu lập bảng tần số cho mẫu số liệu (T) thì có thể hình dung được bức tranh tổng thể về kết quả thi không? Vì sao?
c) Mẫu số liệu (T) được mô tả dưới dạng bảng thống kê sau
| Tổng điểm | < 6 | [6;7) | [7;8) | ... | [28;29) | [29;30) |
| Số thí sinh | 23 | 69 | 192 | ... | 216 | 12 |
Hãy đọc và giải thích số liệu được biểu diễn trong bảng thống kê.
Lời giải:
a) Có 344 752 thí sinh dự thi nên mẫu số liệu về tổng điểm (T) có 344 752 giá trị.
b) Nếu lập bảng tần số cho mẫu số liệu (T) thì không thể hình dung được bức tranh tổng thể về kết quả thi vì tổng điểm thi 3 ba môn của các thí sinh có rất nhiều giá trị khác nhau dẫn đến bảng tần số sẽ dài dòng và phức tạp.
c) Từ bảng thống kê trên ta có thể thấy số lượng thí sinh đạt tổng điểm 3 môn trong từng nhóm điểm. Chẳng hạn
- Số thí sinh có tổng điểm 3 môn nhỏ hơn 6 là 23 thí sinh;
- Số thí sinh có tổng điểm 3 môn từ 6 đến dưới 7 điểm là 69 thí sinh;
...
- Số thí sinh có tổng điểm 3 môn từ 29 đến 30 điểm là 12 thí sinh.
Luyện tập 1 trang 59 Toán 11 Tập 1: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
| Thời gian | [15; 20) | [20; 25) | [25; 30) | [30; 35) | [35; 40) | [40; 45) | [45; 50) |
| Số nhân viên | 6 | 14 | 25 | 37 | 21 | 13 | 9 |
Đọc và giải thích mẫu số liệu này.
Lời giải:
Mẫu số liệu đã cho là mẫu số liệu ghép nhóm gồm 7 nhóm mô tả về thời gian đi từ nhà đến nơi làm việc của các nhân viên một công ty:
- Nhóm 1: Thời gian đi từ 15 phút đến dưới 20 phút, có 6 nhân viên;
- Nhóm 2: Thời gian đi từ 20 phút đến dưới 25 phút, có 14 nhân viên;
- Nhóm 3: Thời gian đi từ 25 phút đến dưới 30 phút, có 25 nhân viên;
- Nhóm 4: Thời gian đi từ 30 phút đến dưới 35 phút, có 37 nhân viên;
- Nhóm 5: Thời gian đi từ 35 phút đến dưới 40 phút, có 21 nhân viên;
- Nhóm 6: Thời gian đi từ 40 phút đến dưới 45 phút, có 13 nhân viên;
- Nhóm 7: Thời gian đi từ 45 phút đến dưới 50 phút, có 9 nhân viên.
2. Ghép nhóm mẫu số liệu
HĐ2 trang 60 Toán 11 Tập 1: Chỉ số BMI (đo bằng w/h2, trong đó w là cân nặng đơn vị kilôgam, h là chiều cao đơn vị là mét) của các học sinh trong một tổ được cho như sau:
![]()
Một người có chỉ số BMI nhỏ hơn 18,5 được xem là thiếu cân; từ 18,5 đến dưới 23 là có cân nặng lí tưởng so với chiều cao; từ 23 trở lên là thừa cân. Hãy lập mẫu số liệu ghép nhóm cho mẫu số liệu trên để biểu diễn tình trạng cân nặng so với chiều cao của các học sinh trong tổ.
Lời giải:
Quan sát mẫu số liệu đã cho, ta thấy:
- Có 1 giá trị BMI của học sinh trong tổ nhỏ hơn 18,5, đó là 16,8;
- Có 5 giá trị BMI của học sinh trong tổ thuộc nửa khoảng từ 18,5 đến 23, đó là 19,2; 21,1; 20,6; 18,7; 19,1;
- Có 2 giá trị BMI của học sinh trong tổ từ 23 trở lên, đó là 23,5; 25,2.
Từ đó ta lập được mẫu số liệu ghép nhóm về tình trạng cân nặng so với chiều cao của các học sinh trong tổ như sau:
| Chỉ số BMI (w/h2) | Dưới 18,5 | Từ 18,5 đến dưới 23 | Từ 23 trở lên |
| Số học sinh | 1 | 5 | 2 |
Luyện tập 2 trang 60 Toán 11 Tập 1: Cân nặng (kg) của 35 người trưởng thành tại một khu dân cư được cho như sau:

Chuyển mẫu số liệu trên thành dạng ghép nhóm, các nhóm có độ dài bằng nhau, trong đó có nhóm [40; 45).
Lời giải:
Độ dài của mỗi nhóm là 45 – 40 = 5.
Giá trị nhỏ nhất là 40, giá trị lớn nhất là 63, do đó, khoảng biến thiên của mẫu số liệu là 63 – 40 = 23. Để cho thuận tiện, ta chọn đầu mút trái của nhóm đầu tiên là 40 và đầu mút phải của nhóm cuối cùng là 65, ta được các nhóm là [40; 45), [45; 50), [50; 55), [55; 60), [60; 65). Đếm số giá trị thuộc mỗi nhóm, ta có mẫu số liệu ghép nhóm như sau:
| Cân nặng (kg) | [40; 45) | [45; 50) | [50; 55) | [55; 60) | [60; 65) |
| Số người | 5 | 7 | 11 | 7 | 5 |
Vận dụng trang 61 Toán 11 Tập 1: Một công ty may quần áo đồng phục học sinh cho biết cỡ áo theo chiều cao của học sinh được tính như sau:
| Chiều cao (cm) | [150; 160) | [160; 167) | [167; 170) | [170; 175) | [175; 180) |
| Cỡ áo | S | M | L | XL | XXL |
Công ty muốn ước lượng tỉ lệ các cỡ áo khi may cho học sinh lớp 11 đã đo chiều cao của 36 học sinh nam khối 11 của một trường và thu được mẫu số liệu sau (đơn vị là centimét):

a) Lập bảng tần số ghép nhóm của mẫu số liệu với các nhóm đã cho ở bảng trên.
b) Công ty may 500 áo đồng phục cho học sinh lớp 11 thì nên may số lượng áo theo mỗi cỡ là bao nhiêu chiếc?
Lời giải:
a) Đếm số giá trị thuộc mỗi nhóm, ta lập được bảng tần số ghép nhóm của mẫu số liệu với các nhóm đã cho ở bảng trên như sau:
| Chiều cao (cm) | [150; 160) | [160; 167) | [167; 170) | [170; 175) | [175; 180) |
| Số học sinh | 0 | 22 | 8 | 6 | 0 |
b) Công ty may 500 áo đồng phục cho học sinh lớp 11 thì nên may số lượng áo theo mỗi cỡ như sau:
- Không nên may áo cỡ S và cỡ XXL;
- Số lượng áo cỡ M nên may là ![]() (chiếc);
(chiếc);
- Số lượng áo cỡ L nên may là ![]() (chiếc);
(chiếc);
- Số lượng áo cỡ XL nên may là 500 – 306 – 111 = 83 (chiếc).
Bài tập
Bài 3.1 trang 61 Toán 11 Tập 1: Trong các mẫu số liệu sau, mẫu nào là mẫu số liệu ghép nhóm? Đọc và giải thích mẫu số liệu ghép nhóm đó.
a) Số tiền mà sinh viên chi cho thanh toán cước điện thoại trong tháng.
| Số tiền (nghìn đồng) | [0; 50) | [50; 100) | [100; 150) | [150; 200) | [200; 250) |
| Số sinh viên | 5 | 12 | 23 | 17 | 3 |
b) Thống kê nhiệt độ tại một địa điểm trong 40 ngày, ta có bảng số liệu sau:
| Nhiệt độ (°C) | [19; 22) | [22; 25) | [25; 28) | [28; 31) |
| Số ngày | 7 | 15 | 12 | 6 |
Lời giải:
a) Mẫu số liệu đã cho là mẫu số liệu ghép nhóm.
Mẫu số liệu này mô tả về số tiền mà sinh viên chi cho thanh toán cước điện thoại trong tháng, gồm có 5 nhóm. Cụ thể:
- Nhóm thanh toán với số tiền từ 0 đến dưới 50 nghìn đồng, có 5 sinh viên;
- Nhóm thanh toán với số tiền từ 50 đến dưới 100 nghìn đồng, có 12 sinh viên;
- Nhóm thanh toán với số tiền từ 100 đến dưới 150 nghìn đồng, có 23 sinh viên;
- Nhóm thanh toán với số tiền từ 150 đến dưới 200 nghìn đồng, có 17 sinh viên;
- Nhóm thanh toán với số tiền từ 200 đến dưới 250 nghìn đồng, có 3 sinh viên;
b) Mẫu số liệu đã cho là mẫu số liệu ghép nhóm.
Mẫu số liệu này mô tả về nhiệt độ tại một địa điểm trong 40 ngày, gồm 4 nhóm nhiệt độ: từ 19 °C đến dưới 22 °C; từ 22 °C đến dưới 25 °C; từ 25 °C đến dưới 28 °C; từ 28 °C đến dưới 31 °C. Cụ thể:
- Có 7 ngày có nhiệt độ từ 19 °C đến dưới 22 °C;
- Có 15 ngày có nhiệt độ từ 22 °C đến dưới 25 °C;
- Có 12 ngày có nhiệt độ từ 25 °C đến dưới 28 °C;
- Có 6 ngày có nhiệt độ từ 28 °C đến dưới 31 °C.
Bài 3.2 trang 61 Toán 11 Tập 1: Số sản phẩm một công nhân làm được trong một ngày được cho như sau:
![]()
Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sáu nhóm có độ dài bằng nhau.
Lời giải:
Giá trị nhỏ nhất của mẫu số liệu là 5, giá trị lớn nhất của mẫu số liệu là 54, do đó khoảng biến thiên của mẫu số liệu là R = 54 – 5 = 49. Ta cần chia thành sáu nhóm với độ dài bằng nhau. Để cho thuận tiện, ta chọn đầu mút trái của nhóm đầu tiên là 3 và đầu mút phải của nhóm cuối cùng bằng 57 và độ dài của mỗi nhóm bằng 9 ta được các nhóm là [3; 12), [12; 21), [21; 30), [30; 39), [39; 48), [48; 57). Đếm số giá trị thuộc mỗi nhóm, ta có mẫu số liệu ghép nhóm như sau:
| Số sản phẩm | [3; 12) | [12; 21) | [21; 30) | [30; 39) | [39; 48) | [48; 57) |
| Số công nhân | 2 | 8 | 8 | 2 | 4 | 1 |
Bài 3.3 trang 61 Toán 11 Tập 1: Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:

Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau.
Lời giải:
Giá trị nhỏ nhất của mẫu số liệu là 492, giá trị lớn nhất của mẫu số liệu là 653, do đó khoảng biến thiên của mẫu số liệu là R = 653 – 492 = 161. Ta cần chia thành bảy nhóm có độ dài bằng nhau. Để cho thuận tiện, ta chọn đầu mút trái của nhóm đầu tiên là 485 và đầu mút phải của nhóm cuối cùng bằng 660 và độ dài của mỗi nhóm bằng 25 ta được các nhóm là [485; 510), [510; 535), [535; 560), [560; 585), [585; 610), [610; 635), [635; 660]. Đếm số giá trị thuộc mỗi nhóm, ta có mẫu số liệu ghép nhóm như sau:
| Thời gian | [485; 510) | [510; 535) | [535; 560) | [560; 585) | [585; 610) | [610; 635) | [635; 660] |
| Số cầu thủ | 8 | 2 | 1 | 2 | 1 | 1 | 1 |

























