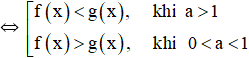Câu hỏi 1 trang 86 SGK
Hãy lập bảng tương tự cho các bất phương trình ax ≥ b, ax < b, ax ≤ b.
Lời giải:
| ax > b | Tập nghiệm | |
| a > 1 | 0 < a < 1 | |
| b ≤ 0 | R | R |
| b > 0 | [logab ; +∞) | (-∞ ; logab] |
| ax < b | Tập nghiệm | |
| a > 1 | 0 < a < 1 | |
| b ≤ 0 | Vô nghiệm | Vô nghiệm |
| b > 0 | (-∞ ; logab) | (logab ; +∞) |
| ax ≤ b | Tập nghiệm | |
| a > 1 | 0 < a < 1 | |
| b ≤ 0 | Vô nghiệm | Vô nghiệm |
| b > 0 | (-∞ ; logab] | [logab ; +∞) |
Câu hỏi 2 trang 87 SGK
Giải bất phương trình 2x + 2-x – 3 < 0.
Lời giải:
Đặt t = 2x (t > 0).
Khi đó: 2x + 2-x – 3 < 0

Câu hỏi 3 trang 88 SGK
Hãy lập bảng tương tự cho các bất phương trình logax ≥ b, logax < b, logax ≤ b.
Lời giải:
| logax ≥ b | a > 1 | 0 < a < 1 |
| Nghiệm | x ≥ ab | 0 < x ≤ ab |
| logax < b | a > 1 | 0 < a < 1 |
| Nghiệm | 0 < x < ab | x > ab |
| logax ≤ b | a > 1 | 0 < a < 1 |
| Nghiệm | 0 < x ≤ ab | x ≥ ab |
Câu hỏi 4 trang 89 SGK
Giải bất phương trình ![]()
Lời giải:

Bài 1 trang 89 SGK
Giải các bất phương trình mũ:

Lời giải:
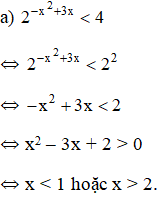
Vậy phương trình có tập nghiệm S = (-∞; 1) ∪ (2; +∞)
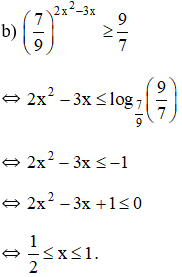
Vậy bất phương trình có tập nghiệm 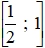
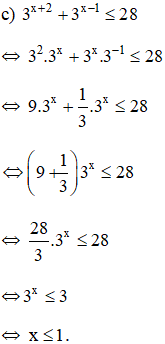
Vậy bất phương trình có tập nghiệm (-∞; 1]
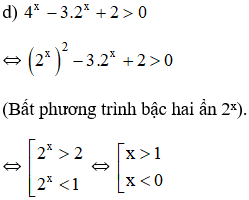
Vậy bất phương trình có tập nghiệm S = (-∞; 0) ∪ (1; +∞)
Kiến thức áp dụng
+ Bất phương trình mũ cơ bản:
| BPT ax < b | BPT ax > b | ||
| b ≤ 0 | PT vô nghiệm | Tập nghiệm là R. | |
| b > 0 | 0 < a < 1 | x > logab | x < logab |
| a > 1 | x < logab | x > logab | |
Bài 2 trang 90 SGK
Giải các bất phương trình lôgarit:
Lời giải:
a) Điều kiện: 4 – 2x > 0 hay x < 2
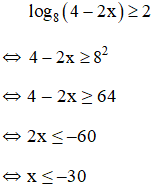
Vậy bất phương trình có tập nghiệm (-∞; -30]

Kết hợp với điều kiện xác định được x > 3.
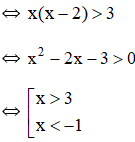
Vậy bất phương trình có tập nghiệm (3; +∞).
d) Điều kiện: x > 0.
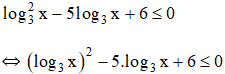
(Bất phương trình bậc hai ẩn log3x).
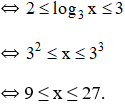
Vậy bất phương trình có tập nghiệm [9; 27].
Kiến thức áp dụng
+ Bất phương trình lôgarit cơ bản
| logaf(x) < b | logaf(x) > b | |
| 0 < a < 1 | f(x) > ab | 0 < f(x) < ab |
| a > 1 | 0 < f(x) < ab | f(x) > ab |
+ Bất phương trình logaf(x) < logag(x)