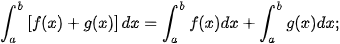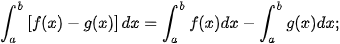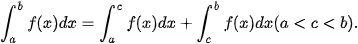(Trang 12)
| THUẬT NGỮ • Tích phân • Cận tích phân • Hàm số dưới dấu tích phân | KIẾN THỨC, KĨ NĂNG • Nhận biết định nghĩa và các tính chất của tích phân. • Tính tích phân trong những trường hợp đơn giản. • Vận dụng tích phân để giải một số bài toán liên quan đến thực tiễn. |
| Một ô tô đang chạy với vận tốc 20 m/s thì người lái đạp phanh. Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc v(t)= -40t +20 (m/s), trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? |  |
1. KHÁI NIỆM TÍCH PHÂN
a) Diện tích hình thang cong
Hình thang cong
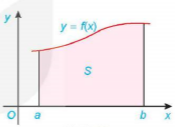
Hình phẳng giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b (a < b), trong đó f(x) là hàm liên tục không âm trên đoạn [a; b], gọi là một hình thang cong.
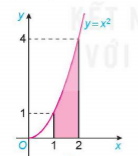
Ví dụ 1. Những hình phẳng được tô màu dưới đây có phải là hình thang cong không?
|
a) |
b) |
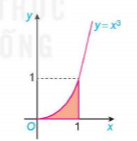
Hình 4.4
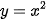
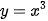
Giải
Hình 4.4a là hình thang cong giới hạn bởi đồ thị 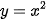 , trục hoành và hai đường thẳng x=1, x = 2.
, trục hoành và hai đường thẳng x=1, x = 2.
Hình 4.4b là hình thang cong giới hạn bởi đồ thị 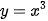 , trục hoành và hai đường thẳng x = 0, x = 1.
, trục hoành và hai đường thẳng x = 0, x = 1.
(Trang 13)
HĐ1. Diện tích của hình thang
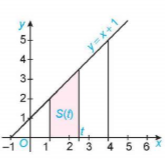
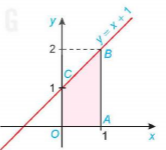
| Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y=x+1, trục hoành và hai đường thẳng x=1, x=t (1≤t≤4) (H.4.3). a) Tính diện tích S của T khi t=4. b) Tính diện tích S(t) của T khi t ∈ [1, 4]. c) Chứng minh rằng S(t) là một nguyên hàm của hàm số f(t) =t+1, t ∈ [1; 4] và diện tích S = S(4) – S(1). |
Hình 4.3 y=x+1 |
HĐ2. Diện tích của hình thang cong
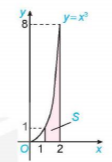
Xét hình thang cong giới hạn bởi đồ thị 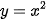 , trục hoành và hai đường thẳng x = 1, x = 2.
, trục hoành và hai đường thẳng x = 1, x = 2.
Ta muốn tính diện tích S của hình thang cong này.
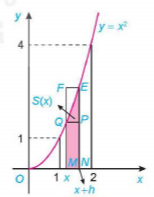
| a) Với mỗi x ∈ [1; 2], gọi S(x) là diện tích phần hình thang cong đã cho nằm giữa hai đường thẳng vuông góc với trục Ox tại điểm có hoành độ bằng 1 và x (H.4.5). Cho h > 0 sao cho x + h < 2. So sánh hiệu S(x + h) − S(x) với diện tích hai hình chữ nhật MNPQ và MNEF (H.4.6). Từ đó suy ra
b) Cho h< 0 sao cho x + h >1. Tương tự phần a, đánh giá hiệu S(x) − S(x + h) và từ đó suy ra
Từ đó chứng minh Người ta chứng minh được S'(1)= 1, S('2)=4, tức là S(x) là một nguyên hàm của d) Từ kết quả của phần c, ta có |
Hình 4.5
Hình 4.6
|
Gọi F(x) là một nguyên hàm tuỳ ý của 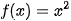 trên [1, 2]. Hãy so sánh S và F(2) – F(1). Tổng quát, ta có:
trên [1, 2]. Hãy so sánh S và F(2) – F(1). Tổng quát, ta có:
(Trang 14)
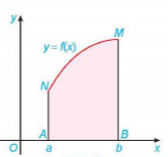
| Định lí 1 Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b là S=F(b) – F(a), trong đó F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a, b]. Ví dụ 2. Tính diện tích S của hình thang cong giới hạn bởi đồ thị hàm số Giải (H.4.8) Một nguyên hàm của hàm số Do đó, diện tích của hình thang cong cần tính là
|
Hình 4.7 y = f(x)
Hình 4.8 |
b) Định nghĩa tích phânHĐ3. Nhận biết khái niệm tích phân Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm tuỳ ý của f(x) trên đoạn [a; b]. Chứng minh rằng F(b) – F(a)=G(b) – G(a). Từ đó, ta có định nghĩa sau: |
Hình 4.8 Chú ý G(x) = F(x) + C, C là hằng số. |
Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a, b] thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là 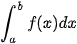 . . |
| Chú ý a) Hiệu F(b) – F(a) thường được kí hiệu là Như vậy | Tích phân không phụ thuộc vào cách kí hiệu biến:
|
b) Ta gọi  là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.
là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.
c) Trong trường hợp a = b hoặc a > b, ta quy ước:
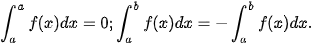
(Trang 15)
Ví dụ 3. Tính:
a) 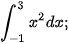
b) 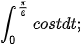
c) 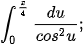
Giải
a) 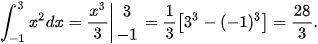
b) 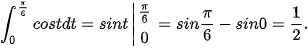
c) 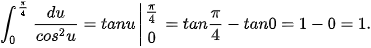
d) 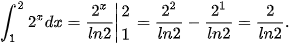
Luyện tập 1. Tính:
a) 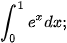
b) 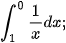
c) 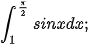
d) 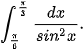
| Từ Định lí 1 và định nghĩa tích phân, ta có Ý nghĩa hình học của tích phân: Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì tích phân
Ví dụ 4. Sử dụng ý nghĩa hình học của tích phân, tính: a) b) Giải: a) Tích phân cần tính là diện tích của hình thang vuông OABC, có đáy nhỏ OC = 1, đáy lớn AB = 2 và đường cao OA = 1 (H.4.10). Do đó:
|
Hình 4.9 y=f(x)
Hình 4.10 y=x+1 |
(Trang 16)
| b) Ta có Vậy Luyện tập 2. Sử dụng ý nghĩa hình học của tích phân, tính: a) b) Vận dụng 1. Giải quyết bài toán ở tình huống mở đầu. |
Hình 4.11
Lưu ý v(t)=s'(t).
|
2. TÍNH CHẤT CỦA TÍCH PHÂN
HĐ4. Nhận biết tính chất của tích phân
Tính và so sánh:
a) 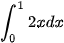 và
và 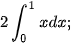
b) 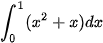 và
và 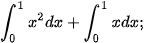
c) 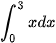 và
và 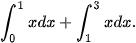
Tính chất của tích phân:
Cho f(x), g(x) là các hàm số liên tục trên đoạn [a; b]. Khi đó, ta có
| 1) 2) 3) 4) |
(Trang 17)
Ví dụ 5. Tính:
a) 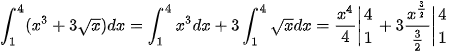
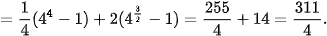
b) 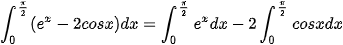
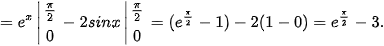
c) 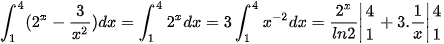
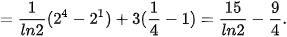
Luyện tập 3. Tính các tích phân sau:
a) 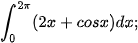
b) 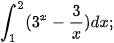
c) 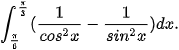
Ví dụ 6. Tính 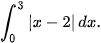
Giải
Ta có:
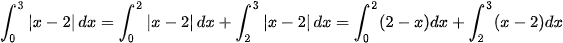
=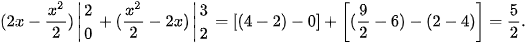
Luyện tập 4. Tính 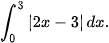
Vận dụng 2. Giá trị trung bình của hàm số liên tục f(x) trên đoạn [a; b] được định nghĩa là
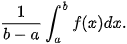
Giả sử nhiệt độ (tính bằng °C) tại thời điểm t giờ trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa ở một địa phương vào một ngày nào đó được mô hình hoá bởi hàm số
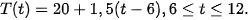
Tìm nhiệt độ trung bình vào ngày đó trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa.
(Trang 18)
BÀI TẬP
4.8. Sử dụng ý nghĩa hình học của tích phân, tính:
a) 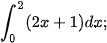
b) 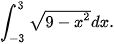
4.9. Cho 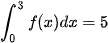 và
và 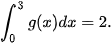 Tính:
Tính:
a) 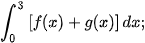
b) 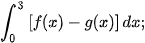
c) 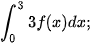
d) 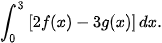
4.10. Tính:
a) 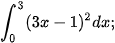
b) 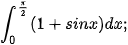
c) 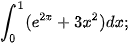
d) 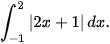
4.11. Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t (giây) là 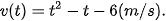
a) Tìm độ dịch chuyển của vật trong khoảng thời gian 1≤t≤ 4, tức là tính 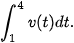
b) Tìm tổng quãng đường vật đi được trong khoảng thời gian này, tức là tính 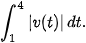
4.12. Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hoá bằng công thức
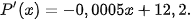
Ở đây P(x) là lợi nhuận (tính bằng triệu đồng) khi bán được x đơn vị sản phẩm.
a) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 101 đơn vị sản phẩm.
b) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 110 đơn vị sản phẩm.
4.13. Giả sử vận tốc v của dòng máu ở khoảng cách r từ tâm của động mạch bán kính R không đổi, có thể được mô hình hoá bởi công thức
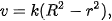
trong đó k là một hằng số. Tìm vận tốc trung bình (đối với r) của động mạch trong khoảng 0≤r≤R. So sánh vận tốc trung bình với vận tốc lớn nhất.
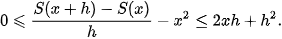
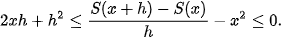
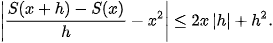
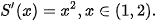
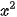 trên [1, 2].
trên [1, 2].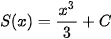 . Sử dụng điều này với lưu ý S(1)=0 và diện tích cần tính S=S(2), hãy tính S.
. Sử dụng điều này với lưu ý S(1)=0 và diện tích cần tính S=S(2), hãy tính S.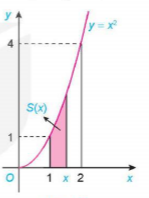
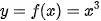 , trục hoành và hai đường thẳng x =1, x = 2.
, trục hoành và hai đường thẳng x =1, x = 2.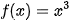 là
là 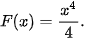
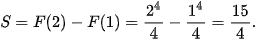

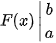
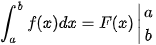 .
.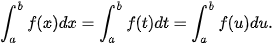

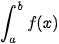 là diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x=a, x = b (H.4.9). Vậy
là diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x=a, x = b (H.4.9). Vậy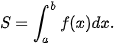
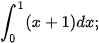
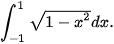
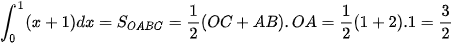
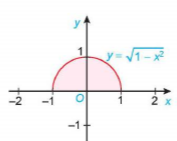
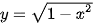 là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc toạ độ O và bán kính 1. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng (H.4.11).
là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc toạ độ O và bán kính 1. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng (H.4.11).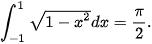
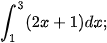
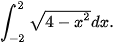

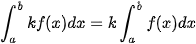 (k là hằng số);
(k là hằng số);