1. Góc giữa hai mặt phẳng, hai mặt phẳng vuông góc
HĐ1 trang 44 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q). Tìm mối quan hệ giữa các góc (a, b) và (a', b').
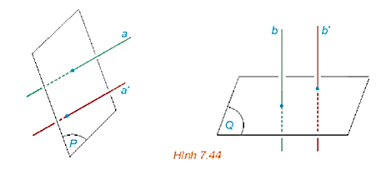
Lời giải:
Vì a ⊥ (P) và a' ⊥ (P) nên a và a' trùng nhau hoặc song song với nhau.
Vì b ⊥ (Q) và b' ⊥ (Q) nên b và b' trùng nhau hoặc song song với nhau.
Do đó (a, b) = (a', b').
Câu hỏi trang 44 Toán 11 Tập 2: Góc giữa hai mặt phẳng bằng 0° khi nào, khác 0° khi nào?
Lời giải:
Xét a ⊥ (P) và b ⊥ (Q).
Khi đó (a, b) là góc giữa hai mặt phẳng (P) và (Q).
Góc giữa hai mặt phẳng (P) và (Q) bằng 0° tức (a, b) = 0° khi a và b song song hoặc trùng nhau hay (P) và (Q) song song hoặc trùng nhau.
Vậy góc giữa hai mặt phẳng bằng 0° khi và chỉ khi hai mặt phẳng đó song song hoặc trùng nhau.
Góc giữa hai mặt phẳng khác 0° khi hai mặt phẳng đó giao nhau.
Luyện tập 1 trang 45 Toán 11 Tập 2: Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, SO ⊥ (ABCD). Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau khi và chỉ khi ABCD là một hình vuông.
Lời giải:
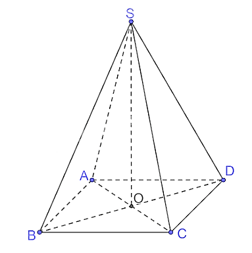
Gọi O là giao điểm của AC và BD.
Vì SO ⊥ (ABCD) nên SO ⊥ AO và SO ⊥ BO mà (SAC) ∩ (SBD) = SO, suy ra góc giữa hai mặt phẳng (SAC) và (SBD) bằng góc giữa hai đường thẳng AO và BO.
Mà (AO, BO) = AOB.
+) Nếu (SAC) ⊥ (SBD) thì AOB = 90°, khi đó AC ⊥ BD mà ABCD là hình chữ nhật, suy ra ABCD là hình vuông.
+) Nếu ABCD là hình vuông thì AC ⊥ BD, suy ra AOB = 90° hay (SAC) ⊥ (SBD).
2. Điều kiện để hai mặt phẳng vuông góc
HĐ2 trang 45 Toán 11 Tập 2: Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q). Lấy một đường thẳng a vuông góc với (P). (H.7.47).
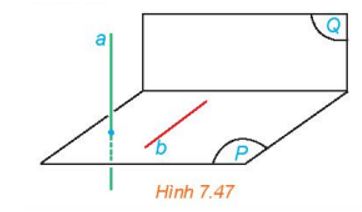
a) Tính góc giữa a và b.
b) Tính góc giữa (P) và (Q).
Lời giải:
a) Vì a ⊥ (P) mà b ⊂ (P) nên a ⊥ b. Vậy (a, b) = 90°.
b) Vì a ⊥ (P) và b ⊥ (Q) nên góc giữa hai mặt phẳng (P) và (Q) bằng góc giữa hai đường thẳng a và b mà (a, b) = 90° nên góc giữa hai mặt phẳng (P) và (Q) bằng 90°.
Luyện tập 2 trang 46 Toán 11 Tập 2: Trong HĐ1 của Bài 23, ta đã nhận ra rằng đường thẳng nối các bản lề của cửa phòng vuông góc với sàn nhà. Hãy giải thích vì sao trong quá trình đóng – mở, cánh cửa luôn vuông góc với sàn nhà.
Lời giải:
Vì mặt phẳng cánh cửa chứa đường thẳng nối các bản lề của cửa phòng, mà đường thẳng nối các bản lề của cửa phòng vuông góc với sàn nhà nên mặt phẳng cánh cửa chứa đường thẳng nối các bản lề của cửa phòng luôn vuông góc với sàn nhà. Do đó trong quá trình đóng – mở, cánh cửa luôn vuông góc với sàn nhà.
3. Tính chất của hai mặt phẳng vuông góc
HĐ3 trang 46 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Kẻ đường thẳng a thuộc (P) và vuông góc với giao tuyến ∆ của (P) và (Q). Gọi O là giao điểm của a và ∆. Trong mặt phẳng (Q), gọi b là đường thẳng vuông góc với ∆ tại O.
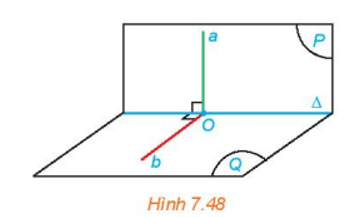
a) Tính góc giữa a và b.
b) Tìm mối quan hệ giữa a và (Q).
Lời giải:
a) Vì a ⊥ ∆ và b ⊥ ∆ mà (P) ∩ (Q) = ∆ nên góc giữa hai mặt phẳng (P) và (Q) bằng góc giữa hai đường thẳng a và b.
Mà góc giữa hai mặt phẳng (P) và (Q) bằng 90° nên (a, b) = 90°.
b) Vì (a, b) = 90° nên a ⊥ b.
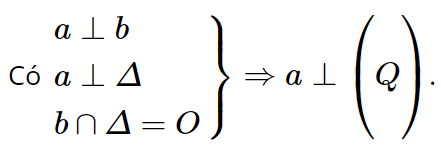
HĐ4 trang 46 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a và cùng vuông góc với mặt phẳng (R). Gọi O là một điểm thuộc a và a' là đường thẳng qua O và vuông góc với (R).
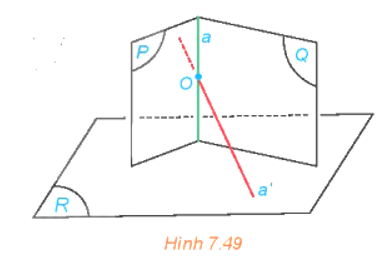
a) Hỏi a' có nằm trong các mặt phẳng (P), (Q) hay không?
b) Tìm mối quan hệ giữa a và a'.
c) Tìm mối quan hệ giữa a và (R).
Lời giải:
a) Vì (P) ⊥ (R) và a' là đường thẳng qua O thuộc (P) mà a' ⊥ (R) nên a' thuộc (P) hay a' nằm trong mặt phẳng (P).
Vì (Q) ⊥ (R) và a' là đường thẳng qua O thuộc (Q) mà a' ⊥ (R) nên a' thuộc (Q) hay a' nằm trong mặt phẳng (Q).
b) Vì a' nằm trong hai mặt phẳng (P) và (Q) nên a' là giao tuyến của hai mặt phẳng (P) và (Q). Lại có theo đề hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a nên a và a' trùng nhau.
c) Vì a' ⊥ (R) mà a và a' trùng nhau nên a ⊥ (R).
Luyện tập 3 trang 47 Toán 11 Tập 2: Với giả thiết như ở Ví dụ 3, Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD). Gọi B', C', D' tương ứng là hình chiếu của A trên SB, SC, SD. Chứng minh rằng:
a) Các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC);
b) Giao tuyến của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
Lời giải:
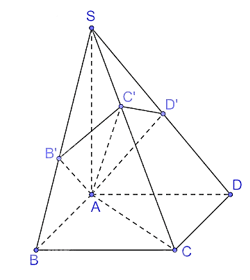
a) Vì B', C', D' tương ứng là hình chiếu của A trên SB, SC, SD nên AB' ⊥ SB, AC' ⊥ SC, AD' ⊥ SD.
Vì SA ⊥ (ABCD) nên SA ⊥ BC, SA ⊥ CD.
Do ABCD là hình chữ nhật nên BC ⊥ AB, CD ⊥ AD.
Vì SA ⊥ BC và BC ⊥ AB nên BC ⊥ (SAB), suy ra (SBC) ⊥ (SAB).
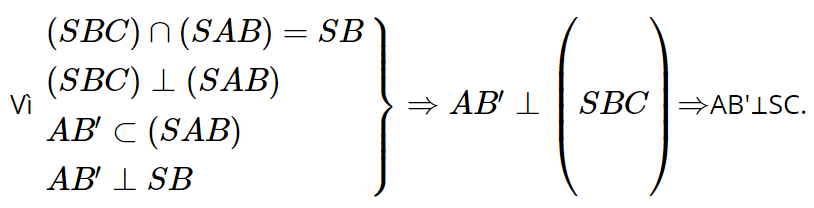
Vì SA ⊥ CD và CD ⊥ AD nên CD ⊥ (SAD), suy ra (SCD) ⊥ (SAD).
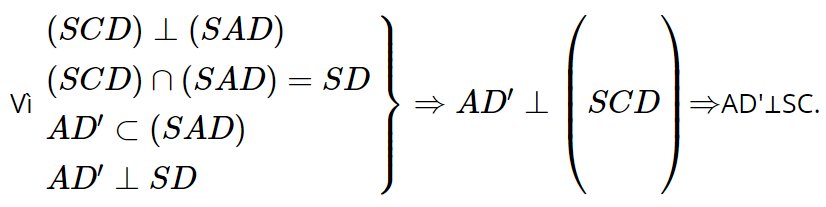
Vì AB′ ⊥ SC và AD′ ⊥ SC nên SC ⊥ (AB'C'D') mà SC ⊂ (SAC) nên (SAC) ⊥ (AB'C'D').
Vì SA ⊥ (ABCD) mà SA ⊂ (SAC) nên (SAC) ⊥ (ABCD).
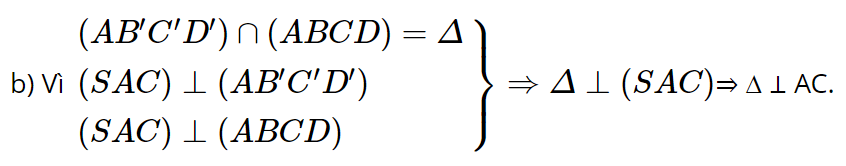
4. Góc nhị diện
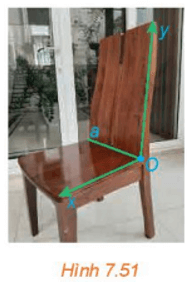
HĐ5 trang 47 Toán 11 Tập 2: Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°. Trong hình 7.51, các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế.
a) Theo tài liệu nói trên, góc nào trong hình bên có số đo từ 100° đến 105°.
b) Nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo từ bao nhiêu đến bao nhiêu độ?
Lời giải:
a) Theo tài liệu nói trên, xOy có số đo từ 100° đến 105°.
b) Vì Ox ⊥ a, Oy ⊥ a nên nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế là góc tạo bởi hai đường thẳng tương ứng chứa Ox và Oy.
Vì 100° ≤ xOy ≤ 105° nên góc giữa hai đường thẳng tương ứng chứa Ox và Oy có thể nhận số đo từ 75° đến 80°.
Vậy góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo từ 75° đến 80°.
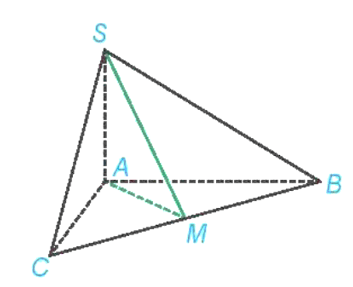
Luyện tập 4 trang 48 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AB = AC = a, ![]() Gọi M là trung điểm của BC.
Gọi M là trung điểm của BC.
a) Chứng minh rằng SMA là một góc phẳng của góc nhị diện [S, BC, A].
b) Tính số đo của góc nhị diện [S, BC, A].
Lời giải:
a) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A mà AM là trung tuyến nên AM là đường cao hay AM ⊥ BC.
Vì SA ⊥ (ABC) nên SA ⊥ BC mà AM ⊥ BC, suy ra BC ⊥ (SAM), do đó BC ⊥ SM.
Vì AM ⊥ BC và BC ⊥ SM nên SMA là một góc phẳng của góc nhị diện [S, BC, A].
b) Áp dụng định lí Côsin cho tam giác ABC, có:
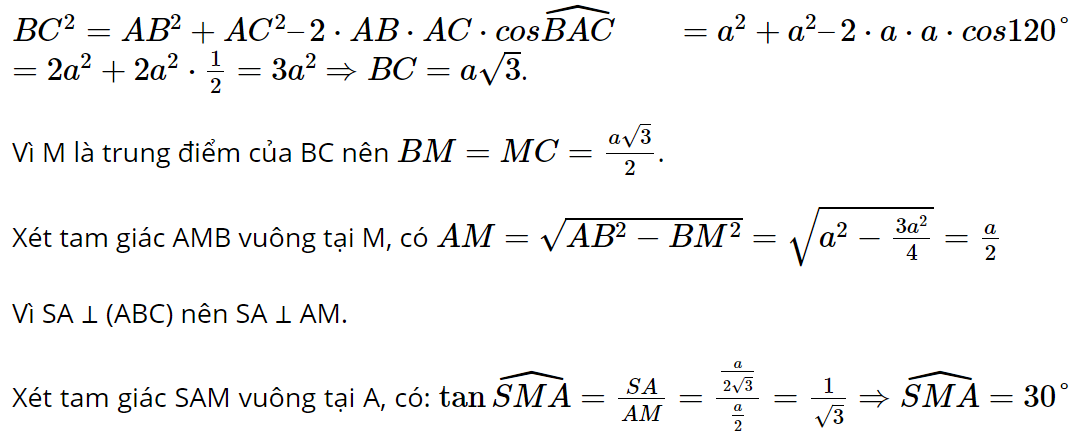
Vậy số đo của góc nhị diện [S, BC, A] bằng 30°.
Vận dụng 1 trang 48 Toán 11 Tập 2: Trong cửa sổ ở Hình 7.56, cánh và khung cửa là các nửa hình tròn có đường kính 80 cm, bản lề được đính ở điểm chính giữa O của các cung tròn khung và cánh cửa. Khi cửa mở, đường kính của khung và đường kính của cánh song song với nhau và cách nhau một khoảng d; khi cửa đóng, hai đường kính đó trùng nhau. Hãy tính số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm.

Lời giải:
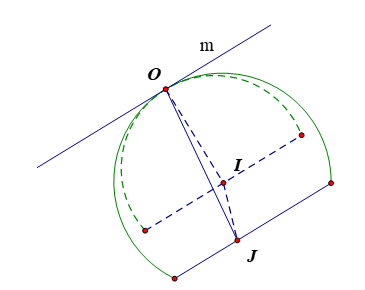
Gọi I, J lần lượt là tâm của nửa hình tròn khung cửa và nửa hình tròn cánh cửa. Khi cửa mở, đường kính của khung và đường kính của cánh song song với nhau, do đó chúng cũng song song với giao tuyến m (qua O) của hai mặt phẳng tương ứng chứa khung và cánh cửa.
Vì O là điểm chính giữa của các cung tròn khung cửa và cánh cửa nên OI vuông góc với đường kính khung cửa, OJ vuông góc với đường kính cánh cửa. Vậy OI, OJ cùng vuông góc với m. Do đó IOJ là một góc phẳng nhị diện của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh và khung cửa.
Vì m ⊥ OI, m ⊥ OJ nên m ⊥ (OIJ) ⇒ m ⊥ IJ.
Vậy IJ cũng vuông góc với các đường kính cánh cửa và khung cửa. Do đó IJ = 40 cm.
Mặt khác OI = OJ = 80 : 2 = 40 cm, suy ra tam giác OIJ đều và IOJ = 60°.
Vậy để khoảng cách d giữa đường kính cánh cửa và đường kính khung cửa bằng 40 cm thì góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh và khung cửa có số đo là 60°.
5. Một số hình lăng trụ đặc biệt
HĐ6 trang 49 Toán 11 Tập 2: Các mặt bên của lăng trụ đứng là các hình gì và các mặt bên đó có vuông góc với mặt đáy không? Vì sao?
Lời giải:
Hình lăng trụ có các mặt bên là hình bình hành.
Mặt khác, hình lăng trụ đứng có các cạnh bên vuông góc với mặt đáy. Do đó hình lăng trụ đứng có các mặt bên là các hình chữ nhật.
Vì các cạnh bên vuông góc với đáy nên mặt bên cũng vuông góc với mặt đáy.
HĐ7 trang 49 Toán 11 Tập 2: Các mặt bên của hình lăng trụ đều có phải là các hình chữ nhật có cùng kích thước hay không? Vì sao?
Lời giải:
Hình lăng trụ đều trước hết là hình lăng trụ đứng nên các mặt bên của nó là các hình chữ nhật.
Mặt khác, các cạnh đáy của lăng trụ đều bằng nhau và các cạnh bên của một lăng trụ luôn bằng nhau. Do đó các mặt bên của hình lăng trụ đều là các hình chữ nhật có cùng kích thước.
HĐ8 trang 49 Toán 11 Tập 2: Trong 6 mặt của hình hộp đứng, có ít nhất bao nhiêu mặt là hình chữ nhật? Vì sao?
Lời giải:
Hình hộp đứng là một trường hợp đặc biệt của hình lăng trụ đứng, có 4 mặt bên là các hình chữ nhật, còn hai đáy là hai hình bình hành. Do đó hình hộp đứng có ít nhất 4 mặt là hình chữ nhật, đó là các mặt bên.
HĐ9 trang 50 Toán 11 Tập 2: a) Hình hộp chữ nhật có bao nhiêu mặt là hình chữ nhật? Vì sao?
b) Các đường chéo của hình hộp chữ nhật có bằng nhau và cắt nhau tại trung điểm mỗi đường hay không? Vì sao?
Lời giải:
a) Hình hộp chữ nhật là hình hộp đứng nên nó có các mặt bên là các hình chữ nhật. Hơn nữa, hai đáy của hình hộp chữ nhật là hai hình chữ nhật. Do đó hình hộp chữ nhật có 6 mặt là hình chữ nhật.
b) Các đường chéo của hình hộp chữ nhật có bằng nhau và cắt nhau tại trung điểm mỗi đường. Bởi vì, cứ hai đường chéo bất kì của hình hộp chữ nhật đều xác định nằm trong một hình chữ nhật và là hai đường chéo của hình chữ nhật đó.
HĐ10 trang 50 Toán 11 Tập 2: Các mặt của một hình lập phương là các hình gì? Vì sao?
Lời giải:
Hình lập phương trước hết là hình hộp chữ nhật nên các mặt đều là hình chữ nhật.
Hơn nữa, nó có tất cả các cạnh bằng nhau nên các mặt là hình vuông.
Vậy các mặt của hình lập phương là hình vuông.
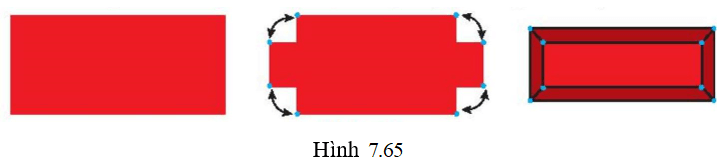
Vận dụng 2 trang 50 Toán 11 Tập 2: Từ một tấm tôn hình chữ nhật, tại 4 góc bác Hùng cắt bỏ đi 4 hình vuông có cùng kích thước và sau đó hàn gắn các mép tại các góc như Hình 7.65. Giải thích vì sao bằng cách đó, bác Hùng nhận được chiếc thùng không nắp có dạng hình hộp chữ nhật.
Lời giải:
Chiếc thùng có đáy và các mặt bên là các hình chữ nhật. Do đó miệng thùng cũng là hình chữ nhật (có các cạnh tương ứng song song và bằng cạnh đáy) thuộc mặt phẳng song song với đáy.
Vì các cạnh bên song song với nhau nên thùng là một hình lăng trụ. Mặt khác, mỗi cạnh bên của thùng đều vuông góc với đáy (vì nó vuông góc với hai cạnh kề của đáy). Do đó thùng là lăng trụ đứng, hơn nữa, có đáy là hình chữ nhật nên thùng có dạng hình hộp chữ nhật.
6. Hình chóp đều và hình chóp cụt đều
HĐ11 trang 51 Toán 11 Tập 2: Tháp lớn tại Bảo tàng Louvre ở Paris (H.7.66) (với kết cấu kính và kim loại) có dạng hình chóp với đáy là hình vuông có cạnh bằng 34 m, các cạnh bên bằng nhau và có độ dài xấp xỉ 32,3 m (theo Wikipedia.org).
Giải thích vì sao hình chiếu của đỉnh trên đáy là tâm của đáy tháp.

Lời giải:
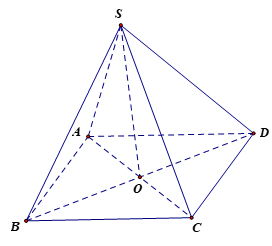
Giả sử tháp có dạng hình chóp S.ABCD với đáy là hình vuông và các cạnh bên bằng nhau.
Theo đề có: AB = BC = CD = DA = 34 m, SA = SB = SC = SD ≈ 32,3 m.
Gọi O là hình chiếu của S trên mặt đáy nên SO ⊥ (ABCD).

Mà SA = SB = SC = SD nên OA = OB = OC = OD hay O là tâm đường tròn ngoại tiếp hình vuông ABCD, do đó O là tâm của hình vuông.
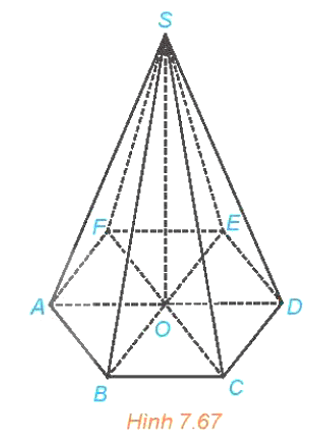
HĐ12 trang 51 Toán 11 Tập 2: Cho hình chóp S.A1A2…An. Gọi O là hình chiếu của S trên mặt phẳng (A1A2…An) (H.7.67).
a) Trong trường hợp hình chóp đã cho là đều, vị trí của điểm O có gì đặc biệt đối với đa giác đều A1A2…An?
b) Nếu đa giác A1A2…An là đều và O là tâm của đa giác đó thì hình chóp đã cho có gì đặc biệt?
Luyện tập 5 trang 51 Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng ![]() . Tính số đo góc nhị diện [S, BC, A].
. Tính số đo góc nhị diện [S, BC, A].
Lời giải:
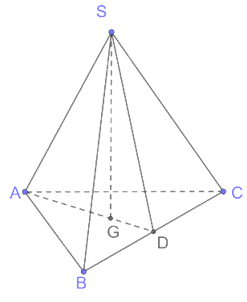
Gọi G là hình chiếu của S trên mặt phẳng (ABC).
Vì S.ABC là hình chóp tam giác đều nên G là trọng tâm của tam giác ABC.
Gọi AG cắt BC tại D mà ABC là tam giác đều nên AD ⊥ BC.
Mà SG ⊥ (ABC) nên SG ⊥ BC.
Vì AD ⊥ BC và SG ⊥ BC nên BC ⊥ (SAD), suy ra BC ⊥ SD.
Vì AD ⊥ BC và BC ⊥ SD nên SDAmlà góc phẳng nhị diện của góc nhị diện [S, BC, A].
Vì ABC là tam giác đều cạnh a, AD là đường cao nên ![]()
Suy ra ![]()
Xét tam giác ABC có AD là trung tuyến nên D là trung điểm của BC, do đó ![]()
Xét tam giác SBD vuông tại D có 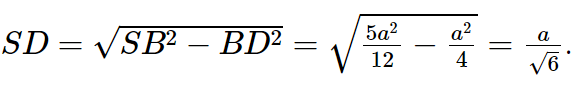
Xét tam giác SGD vuông tại G có 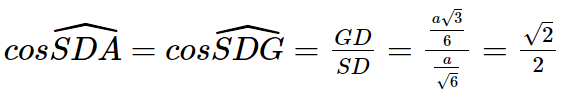
![]()
Vậy số đo góc nhị diện [S, BC, A] là 45°.
HĐ13 trang 52 Toán 11 Tập 2: Cho hình chóp đều S.A1A2…An. Một mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh S.A1A2…An tương ứng tại B1, B2…, Bn (H.7.69).
a) Giải thích vì sao S.B1B2…Bn là một hình chóp đều.
b) Gọi H là tâm của đa giác A1A2…An. Chứng minh rằng đường thẳng SH đi qua tâm K của đa giác đều B1B2…Bn và HK vuông góc với các mặt phẳng (A1A2…An), (B1B2…Bn).
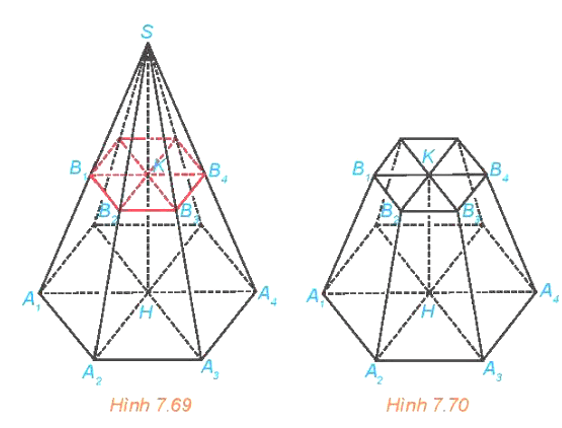
Lời giải:

Câu hỏi trang 52 Toán 11 Tập 2: Hình chóp cụt đều có các cạnh bên bằng nhau hay không?
Lời giải:
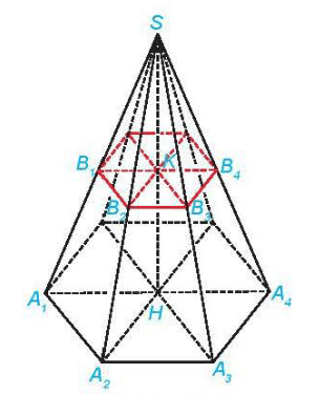
Hình chóp cụt đều có các cạnh bên bằng nhau vì:
A1B1 = SA1 – SB1; A2B2 = SA2 – SB2; …; AnBn = SAn – SBn.
Dựa vào kết quả của hoạt động 13, ta có: SA1 = SA2 = … = SAn và SB1 = SB2 = …= SBn nên A1B1 = A2B2 = AnBn.

























