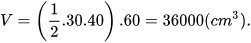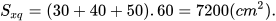(Trang 81)
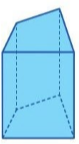
Trong thực tiễn ta thường gặp những đồ vật có hình khối như ở Hình 18 và Hình 19.
|
Hình 18 |
Hình 19 |
| Những hình khối có dạng như trên được gọi là hình gì? |  |
I. HÌNH LĂNG TRỤ ĐỨNG TAM GIÁC
1 Thực hiện các hoạt động sau:
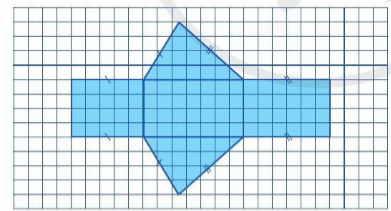
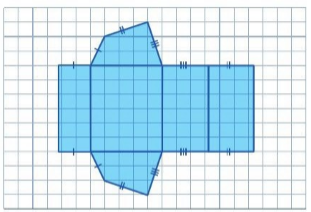
a) Vẽ trên giấy kẻ ô vuông hai hình tam giác và ba hình chữ nhật như ở Hình 20;
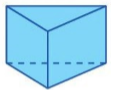
b) Cắt rời theo đường viền của hình vừa vẽ (phần tô màu) và gấp lại để nhận được hình khối như ở Hình 21. Những hình khối như thế gọi là hình lăng trụ đứng tam giác (còn gọi tắt là lăng trụ đứng tam giác).
|
Hình 20 |
Hình 21 |
c) Quan sát lăng trụ đứng tam giác ở Hình 21, nêu số mặt, số cạnh và số đỉnh của lăng trụ đứng tam giác đó.
Nhận xét: Lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
(Trang 82)
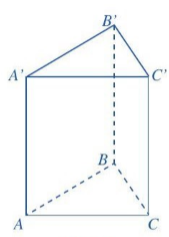
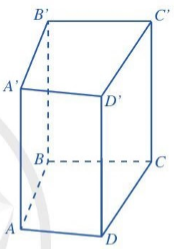
| 2 Quan sát lăng trụ đứng tam giác ở Hình 22, đọc tên các mặt, các cạnh và các đỉnh của lăng trụ đứng tam giác đó. Ở Hình 22, ta có: • Lăng trụ đứng tam giác ABC.A'B'C'; • Đáy dưới ABC, đáy trên A'B'C’; Các mặt bên: AA'B'B, BB'C'C, CC'A'A; • Các cạnh đáy: AB, BC, CA, A’B’, B’C’, C’A’; Các cạnh bên: AA’, BB', CC'; • Các đỉnh: A, B, C, A’, B’, C’. |
Hình 22 |
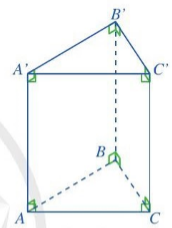
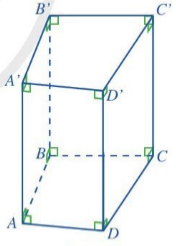
| 3 Quan sát lăng trụ đứng tam giác ABC.A’B'C' ở Hình 23 và cho biết: a) Đáy dưới ABC và đáy trên A’B′C′ là hình gì? b) Mặt bên AA’C’C là hình gì? c) So sánh độ dài hai cạnh bên AA’ và CC’. Nhận xét Lăng trụ đứng tam giác có: • Hai mặt đáy cùng là tam giác và song song với nhau; Mỗi mặt bên là hình chữ nhật; • Các cạnh bên bằng nhau; • Chiều cao của hình lăng trụ đứng tam giác là độ dài một cạnh bên. Chẳng hạn, ở Hình 23, chiều cao của hình lăng trụ đứng tam giác ABC.A’B’C’ chính là độ dài cạnh bên AA’. |
Hình 23 |
II. HÌNH LĂNG TRỤ ĐỨNG TỨ GIÁC
4 Thực hiện các hoạt động sau:
a) Vẽ trên giấy kẻ ô vuông hai hình tứ giác và bốn hình chữ nhật với vị trí và các kích thước như ở Hình 24.
b) Cắt rời theo đường viền của hình vừa vẽ (phần tô đậm) và gấp lại để nhận được hình khối như ở Hình 25. Những hình khối như thế gọi là hình lăng trụ đứng tứ giác (còn gọi tắt là lăng trụ đứng tứ giác).
(Trang 83)
|
Hình 24 |
Hình 25 |
c) Quan sát lăng trụ đứng tứ giác ở Hình 25, nêu số mặt, số cạnh và số đỉnh của lăng trụ đứng tứ giác đó.
Nhận xét: Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.
| 5 Quan sát lăng trụ đứng tứ giác ở Hình 26, đọc tên các mặt, các cạnh và các đỉnh của lăng trụ đứng tứ giác đó. Ở Hình 26, ta có: • Lăng trụ đứng tứ giác ABCD.A'B'C'D'; • Đáy dưới ABCD, đáy trên A'B'C'D'; Các mặt bên: AA'B'B, BB'C'C, CC'D'D, DD'A’A; • Các cạnh đáy: AB, BC, CD, DA, A'B', B'C', C'D',D'A'; Các cạnh bên: AA', BB', CC’, DD’; • Các đỉnh: A, B, C, D, A', B', C’, D’. |
Hình 26 |
| 6 Quan sát lăng trụ đứng tứ giác ABCD.A'B'C'D' ở Hình 27 và cho biết: a) Đáy dưới ABCD và đáy trên A’B’C’D' là hình gì? b) Mặt bên AA’D’D là hình gì? c) So sánh độ dài hai cạnh bên AA’ và DD’. Nhận xét: Lăng trụ đứng tứ giác có: • Hai mặt đáy cùng là tứ giác và song song với nhau; Mỗi mặt bên là hình chữ nhật; • Các cạnh bên bằng nhau; • Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên. Chẳng hạn, ở Hình 27, chiều cao của hình lăng trụ đứng tứ giác ABCD.A'B'C'D' chính là độ dài cạnh bên AA'. |
Hình 27 |
 Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác. |
(Trang 84)
III. THỂ TÍCH VÀ DIỆN TÍCH XUNG QUANH CỦA HÌNH LĂNG TRỤ ĐỨNG TAM GIÁC, LĂNG TRỤ ĐỨNG TỨ GIÁC
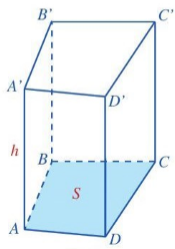
| 7 Nêu công thức tính thể tích hình hộp chữ nhật ABCD.A'B'C'D'. Đối với hình lăng trụ đứng tứ giác, cách tính thể tích cũng tương tự như cách tính thể tích của hình hộp chữ nhật.
| Hình 28 |
Tức là:
V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác (Hình 28).
Tương tự, ta có:
 Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao. |
Tức là:
V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác (Hình 29).
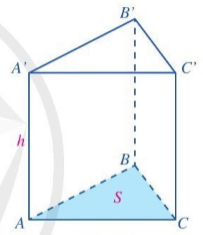
Hình 29
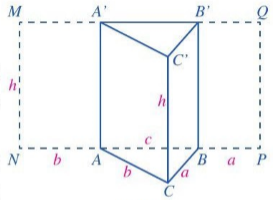
| 8 Quan sát hình lăng trụ đứng tam giác (Hình 30). Trải mặt bên AA’C’C thành hình chữ nhật AA’MN. Trải mặt bên BB'C'C thành hình chữ nhật BB'QP. a) Tính diện tích hình chữ nhật MNPQ. b) So sánh diện tích của hình chữ nhật MNPQ với tích của chu vi đáy của hình lăng trụ đứng tam giác ABC.A'B'C' và chiều cao của hình lăng trụ đó. c) So sánh diện tích của hình chữ nhật MNPQ với diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A'B'C'. |
Hình 30 |
(Trang 85)
Như vậy ta có:
| Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao. |
Tức là:
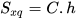, trong đó 
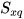là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.
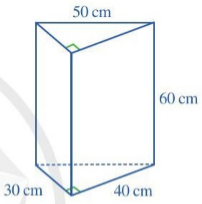
Ví dụ Cho hình lăng trụ đứng tam giác với hai đáy là hai tam giác vuông và các kích thước như ở Hình 31. Tính thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác đó.
| Giải Thể tích của hình lăng trụ đứng tam giác đó là:
Diện tích xung quanh của hình lăng trụ đứng tam giác đó là:
|
Hình 31 |
BÀI TẬP
1. Tìm số thích hợp cho 
trong bảng sau:
| Hình lăng trụ đứng tam giác | Hình lăng trụ đứng tứ giác | |
| Số mặt | | |
| Số đỉnh | | |
| Số cạnh | | |
| Số mặt đáy | | |
| Số mặt đáy | | |
(Trang 86)
2. Chọn từ “đúng (Đ)”, “sai (S)” thích hợp cho trong bảng sau:
| Hình lăng trụ đứng tam giác | Hình lăng trụ đứng tứ giác | |
| Các mặt đáy song song với nhau | | |
| Các mặt đáy là tam giác | | |
| Các mặt đáy là tứ giác | | |
| Các mặt bên là hình chữ nhật | | |
| Thể tích bằng diện tích đáy nhân với độ dài cạnh bên | | |
| Diện tích xung quanh bằng chu vi đáy nhân với độ dài cạnh bên | | |
3. Cho các hình 32a, 32b, 32c:
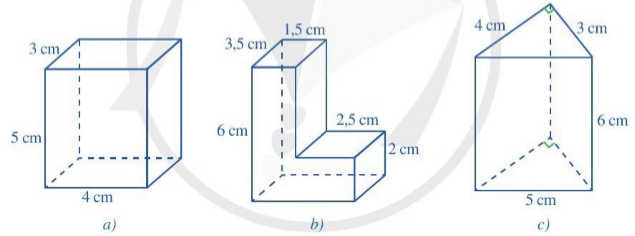
Hình 32
(i) Hình nào trong các hình 32a, 32b, 32c là hình lăng trụ đứng tam giác? Hình lăng trụ đứng tứ giác?
(ii) Tính diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác có ở Hình 32.
(iii) Tính thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác có ở Hình 32.
