Các hàm số lượng giác thường được dùng để mô tả những hiện tượng thay đổi một cách tuần hoàn hay gặp trong thực tiễn, khoa học và kĩ thuật. Trong bài này, ta tìm hiểu các hàm số lượng giác y = sinx, y = cosr, y = tanx, y = cotx.
1. Các hàm số y = sinx và y = cos.r:
H1 Trên hình 1.1, hãy chỉ ra các đoạn thẳng có độ dài đại sổ bằng sinx, bằng cos.r. Tính sin π/2, cos (-π/4), cos2π.
a) Định nghĩa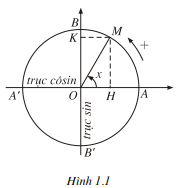
Quy tắc đặt tương ứng mỗi số thực x với sin của góc lượng giác có số đo radian bằng x được gọi là hàm số sin, kí hiệu là y = sin.x. Quy tắc đặt tương ứng mỗi số thực x với côsin của góc lượng giác có số đo radian bằng x được gọi là hàm số côsin, kí hiệu là y = cosx.
Tập xác định của các hàm số y = sin x, y = cosx là R. Do đó các hàm số sin và côsin được viết là sin:
R → R x → sinx
cos : R → R x → cos.x.
Nhận xét: Hàm số y = sin x là một hàm số lẻ vì sin(-x) = -sin x với mọi x thuộc IR.
H2 Tại sao có thể khẳng định hàm số y = cos x là một hàm số chẵn ?
b) Tính chất tuần hoàn của các hàm số y = sin x và y = cos x
Ta đã biết, với mỗi số nguyên k, số k2m thoa mãn
sin(x + k2m) = sinx với mọi x.
Ngược lại, có thể chứng minh rằng số T sao cho
sin(x + T) = sinx với mọi x
phai có dạng T = K2m, k là một số nguyên.
Rõ ràng, trong các số dạng k2m (k e Z), số dương nhỏ nhất là 2m.
Vậy đối với hàm số y = sin.x, số T = 2t là số dương nhỏ nhất thoa mãn sin (x + T) = sin.x với mọi x.
Hàm số y = cos x cũng có tính chất tương tự.
Ta nói hai hàm số đó là những hàm số tuần hoàn với chu kì 2m.
Từ tính chất tuần hoàn với chu kì 2m, ta thấy khi biết giá trị các hàm số y = sin.x và y = cos.r trên một đoạn có độ dài 2m (chẳng hạn đoạn [0 ; 2m] hay đoạn [-r ; x]) thì ta tính được giá trị của chúng tại mọi x. (Cứ mỗi khi biến số được cộng thêm 2m thì giá trị của các hàm số đó lại trở về như cũ; điều này giải thích từ "tuần hoàn").
c) Sự biến thiên và đồ thị của hàm số y = sinx
Do hàm số y = sinx là hàm số tuần hoàn với chu kì 2m nên ta chỉ cần khảo sát hàm số đó trên một đoạn có độ dài 2, chẳng hạn trên đoạn [-n ; x].
• Chiều biến thiên (xem các hình 1.2, 1.3, 1.4)
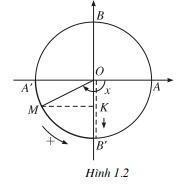
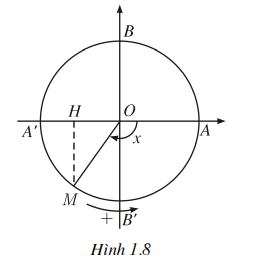
Cho x = (OA, OM) tăng từ -í đến t, tức là cho M chạy trên đường tròn lượng giác theo chiều dương một vòng xuất phát từ A' và quan sát sự thay đổi của điểm K (K là hình chiếu của M trên trục sin, OK = sinx), ta thấy :
- Khi x tăng từ -* đến _T thì điểm M chạy trên đường tròn lượng giác
theo chiều dương từ A' đến B' và điểm K chạy dọc trục sin từ O đến B'. Do đó
OK, tức là sin x, giảm từ 0 đến -1 (h. 1.2).
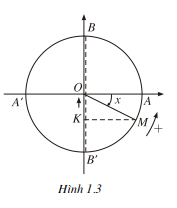
- Khi x tăng từ -pi/2 đến pi/2 thì diểm M chạy trên dường tròn lượng giác theo chiều dương từ B' đến B và điểm K chạy dọc trục sin từ B' đến B. Do đó
OK, tức là sin.x, tăng từ -1 đến 1 (h. 1.3).
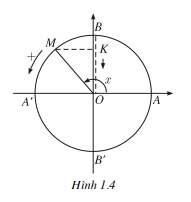
- Khi x tăng từ pi/2, đến t thì điểm M chạn
trên đường tròn lượng giác theo chiêu dương từ B đến A' và điểm K chạy dọc trục
sin từ B đến O. Do đó OK, tức là sin x, giảm từ 1 đến 0 (h. 1.4).
Vậy ta có bảng biến thiên của hàm số y = sinx trên đoạn [-π; π) như sau :
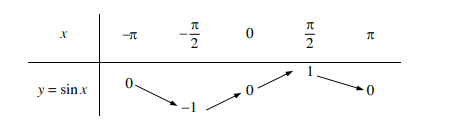
• Đồ thị
- Khi vẽ đồ thị của hàm số y = sin x trên đoạn [-π; π), ta nên để ý rằng :
Hàm số y = sinx là một hàm số lẻ, do đó đồ thị của nó nhận gốc toạ độ làm tâm đối xứng. Vì vậy, đầu tiên ta vẽ đồ thị của hàm số y = sin x trên
doan ［0;π］.
Trên đoạn [0; ], đồ thị của hàm số y = sin.x (h. 1.5) đi qua các điểm có toạ độ (x ; y) trong bảng sau :
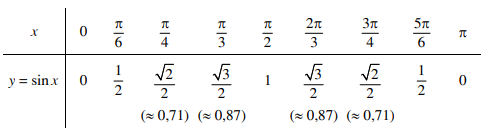
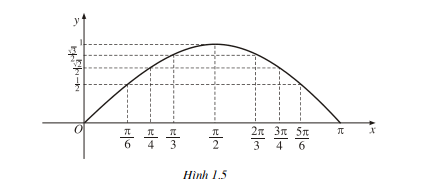
Phần đồ thị của hàm số y = sin x trên đoạn [0;π ] cùng với hình đối xứng của nó qua gốc O lập thành đồ thị của hàm số y = sin x trên đoạn [-π ; π) (h.1.6).
- Tịnh tiến phần đồ thị vừa vẽ sang trái, sang phải những đoạn có độ dài 2π,4π, 6π,... thì được toàn bộ đồ thị hàm số y = sin.x. Đồ thị đó được gọi là một đường hình sin (h. 1.6).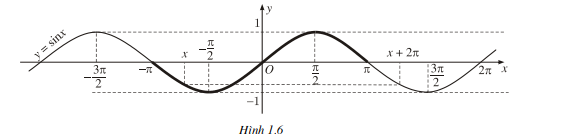
Nhận xét
1) Khi x thay đổi, hàm số y = sin x nhận mọi giá trị thuộc đoạn [-1 ; 1]. Ta nói tập giá trị của hàm số y = sin x là đoạn [-1 ; 1).
2) Hàm số y=sinx đồng biến trên khoảng (-π/2; π/2 ). Từ đó, do tính chấttuần hoàn với chu kì 2m, hàm số y= sin.x đồng biến trên mỗi khoảng（-π/2 + k2π）（π/2 + k2π）
H3 Hỏi khẳng định sau đây có đúng không? Vì sao ?Hams 6 y sin nghich biten ten thoing (1 5) va nghich bien ten me thoangE +127: +127 ). k E2.
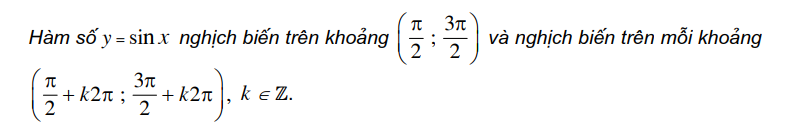
d) Sự biến thiên và đồ thị của hàm số y = cos x
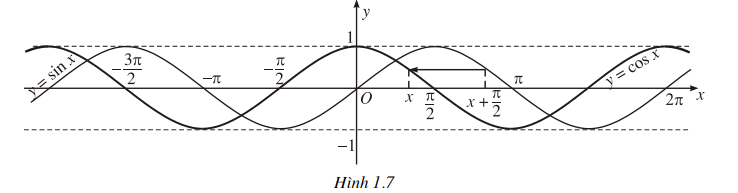
Ta có thể tiến hành khảo sát sự biến thiên và vẽ đồ thị của hàm số y = cos.x tương tự như đã làm đối với hàm số y = sin x trên đây. Tuy nhiên, ta nhận thấy cosx = sin( x + π/2) với mọi x, nên bằng cách tịnh tiến dổ thị hàm số y = sin x sang trái một đoạn có độ dài π/2, ta được đồ thị hàm số y = cos.r (nó cũng được gọi là một đường hình sin) (h. 1.7).
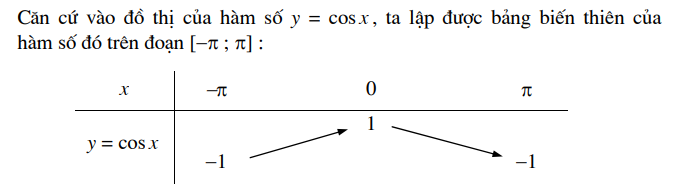
H4 Hãy kiểm nghiệm lại bảng biến thiên trên bằng cách quan sát chuyển động của điểm H trên trục côsin, trong đó H là hình chiếu của điểm M trên trục côsin, khi điểm M chạy trên đường tròn lượng giác theo chiều dương một vòng xuất phát từ điểm A' (h. 1.8).
Nhận xét
1) Khi x thay đổi, hàm số y = cosx nhận mọi giá trị thuộc đoạn [-1 : 1). Ta nói tập giá trị của hàm số y = cos x là đoạn [-1 ; 1).
2) Do hàm số y = cos x là hàm số chẵn nên đồ thị của hàm số y = cos x nhận trục tung làm trục đối xứng.
2. Các hàm số y = tan x và y = cot x
a) Định nghĩa
Quy tác đặt tương ứng mỗi số x e 22 với số thực cot x = COS.x được gọi là hàm số côtang, kí hiệu là y = cot .x.
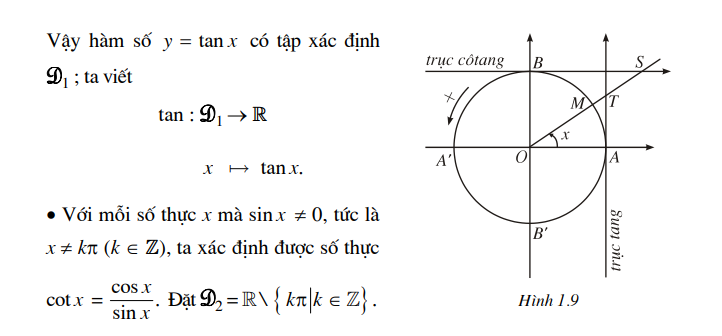
Vậy hàm số y = cot x có tập xác định là D2 ; ta viết
cot : 92 → R
x → cotx.
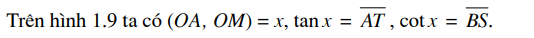
Nhận xét
1) Hàm số y = tanx là một hàm số lẻ vì nếu x e 9, thì -x e Đ, vàtan(-x) = -tan.x.
2) Hàm số y = cot.x cũng là một hàm số lẻ vì nếu x e 92 thì -x e D2 vàcot(-x) = -cot.x.
b) Tính chất tuần hoàn
C) Sự biến thiên và đồ thị của hàm số y = tan x
Do tính chất tuần hoàn với chu kì í của hàm số y = tan.x, ta chỉ cần khảo sát sự biến thiên và về đổ thị của nó trên khoảng (-5 F) c Đ, rồi tịnh tiến phần đồ thị vừa vẽ sang trái, sang phải các đoạn có độ dài π, 2π, 3π,... thì được toàn bộ đồ thị của hàm số y = tan x.
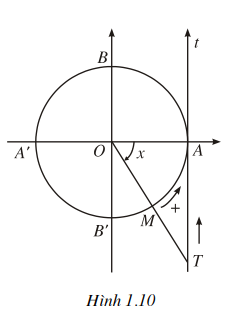
• Chiều biến thiên (h. 1.10) : Khi cho x = (OA, OM) tăng từ -π/2 đến π/2 , (không kể -π/2 và π/2) thì điểm M1 chạy trên đường tròn lượng giác theo chiều dương
A' từ B' đến B (không kể B' và B). Khi đó điểm T thuộc trục tang At sao cho AT = tan.x chạy dọc theo At suốt từ dưới lên trên, nên tan x tăng từ -oo đến +oo (qua giá trị 0 khi x = 0).
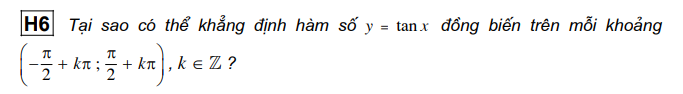
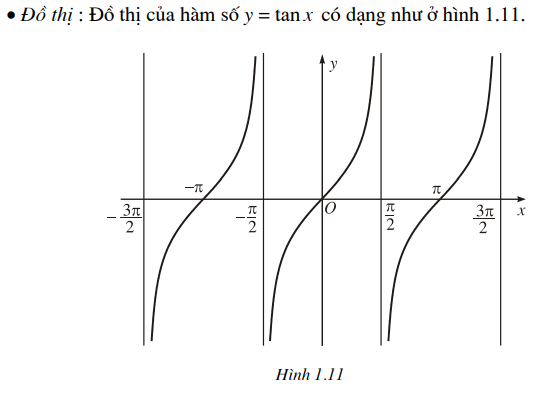
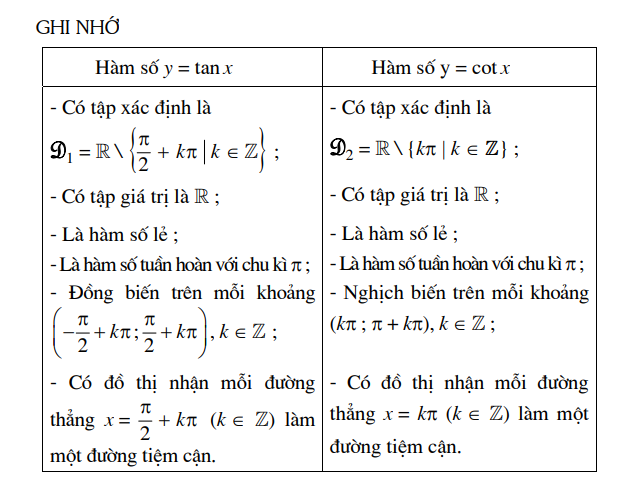
Nhận xét 1) Khi x thay đổi, hàm số y = tan x nhận mọi giá trị thực. Ta nói tập giá trị của hàm số y = tan x là R. 2) Vì hàm số y = tan x là hàm số lẻ nên đồ thị của nó nhận gốc toạ độ làm tâm đối xứng. 3) Hàm số y = tanr không xác định tại x = *, + k* (k € Z). Với mỗi k e Z. đường thẳng vuống gốc với trục hoành, đi qua điem (E + k7 0) gọi là mội đường tiệm cận của đồ thị hàm số y = tan x. (Từ "tiệm cận" có nghĩa là ngày càng gần. Chẳng hạn nối đường thẳng x = - là một đường tiệm cận của dồ thị hàm số y = tan x nhằm diễn tả tính chất : điểm M trên đồ thị có hoành độ càng gần [ thì M càng gần dường thẳng x = E). d) Sự biến thiên và đồ thị của hàm số y = cot x
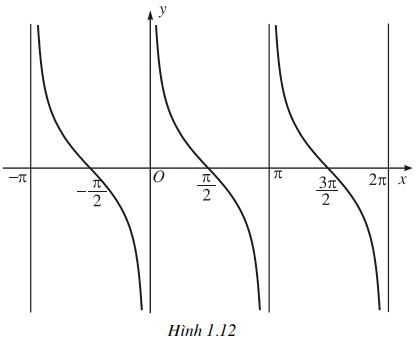
Hàm số y = cot x xác định trên D2 = R \(kn | k € Z) là một hàm số tuần hoàn với chu kì r. Ta có thể khảo sát sự biến thiên và vẽ đồ thị của nó tương tự như đã làm đối với hàm số y = tan x. Đồ thị của hàm số y = cot x có dạng như hình 1.12. Nó nhận mỗi đường thẳng vuông góc với trục hoành, đi qua điểm (kn; 0), k e Z, làm một đường tiệm cận.
3. Về khái niệm hàm số tuần hoàn
Các hàm số y = sinx, y = cosx là những hàm số tuần hoàn với chu kì 2m ; các hàm số y = tan x, y = cotx là những hàm số tuần hoàn với chu kì n. Một cách tổng quát : •Hàm số y = f(x) xác định trên tập hợp 9 được gọi là hàm số tuần hoàn nếu có số T 0 sao cho với mọi x e 9 ta có x+ T € 9, x- T € 9 và f.x + T) = f(x). Nếu có số T dương nhỏ nhất thoa mãn các điều kiện trên thì hàm số đó được gọi là một hàm số tuần hoàn với chu kì T.
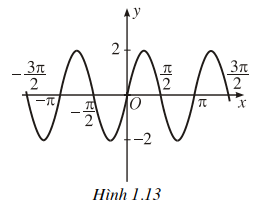
Ví dụ. Các hàm số y = 2sin 2x (đồ thị ở hình 1.13), hàm số y = sin * (đồ thị ở hình 1.14), và hàm số có đồ thị ở hình 1.15 là những hàm số tuần hoàn.
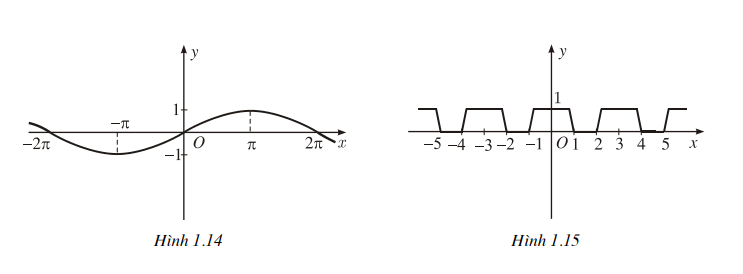
CÂU HỎI VÀ BÀI TẬP
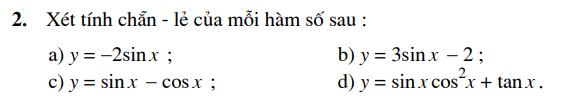
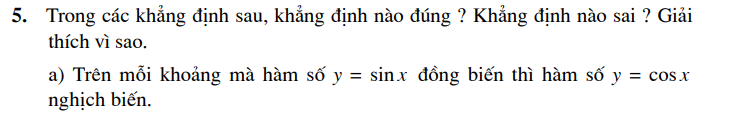
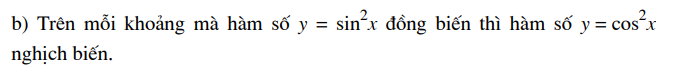
Bài đọc thêm
DAO ĐỘNG ĐIỀU HOA
Nhiều hiện tượng tự nhiên thay đổi có tính chất tuần hoàn (lặp đi lặp lại sau khoảng thời gian xác định) như :
- Chuyển động của các hành tinh trong hệ mặt trời,
- Chuyển động của guồng nước quay,
- Chuyển động của quả lắc đồng hồ,
- Sự biến thiên của cường độ dòng điện xoay chiều,....
Hiện tượng tuần hoàn đơn giản nhất là dao động điều hòa được mô tả bởi hàm số
y = Asin(ax + a) + B,
trong đó A, B, c và a là những hằng số; A và o khác 0. Đó là hàm số tuần hoàn với chu kì 2ã : 141 gọi là biên độ. Đổ thị của nó là một đường hình sin có được từ đổ thị
của hàm số y = Asinon bằng cách tinh tiến thích hợp (theo vecto --
2= rồi theo
vectơ Bì , tức là tịnh tiến theo vecto -97 + Bì)
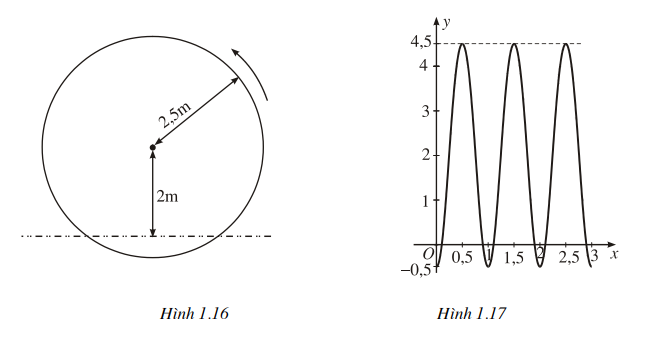
Ví dụ. Một guồng nước có bán kính 2,5m, có trục quay ở cách mặt nước 2m, quay đều mỗi phút một vòng (h. 1.16). Gọi y (mét) là "khoảng cách" từ mặt nước đến một chiếc gầu của guồng nước ở thời điểm x (phút) (quy ước rằng y > 0 khi gầu ở bên trên mặt nước và y < O khi gầu ở dưới nước). Biết rằng sau khi khởi động ≥ phút thì chiếc gầu đó ở đỉnh cao nhất của guồng nước. Từ các điều đó ta suy ra y=2+25si 25（1-米）. Đồ thị của hàm số này có dạng như ở hình 1.17.
LUYỆN TẬP
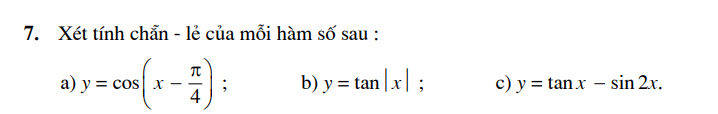
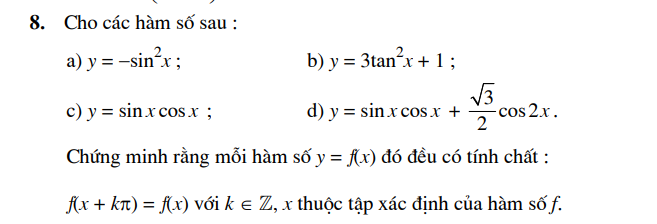
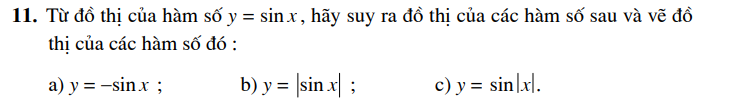
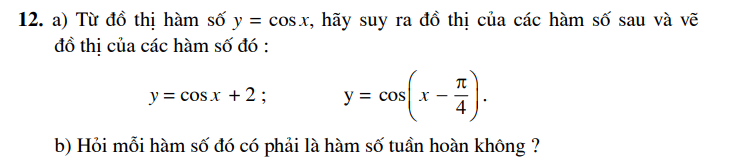
ÂM THANH
Âm thanh được tạo nên bởi sự thay đổi áp suất của môi trường vật chất (chất khí, chất lỏng, chất rắn) một cách tuần hoàn theo thời gian (dao động tuần hoàn) và được lan truyền trong môi trường đó (sóng âm thanh).
Nếu dao động tuần hoàn ấy có chu kì T (đo bằng đơn vị thời gian là giây) thì ÷ gọi
là tần số của dao động (tức là số chu kì trong một giây) ; đơn vị của tần số là Héc (Hertz) viết tắt là Hz. Ăm thanh tai người nghe được là dao động có tần số trong khoảng từ 17-20 Hz đến 20 000 Hz. Dao động có tần số cao hơn 20 000 Hz được gọi là siêu âm.
Trong âm nhạc (nghệ thuật phối hợp các âm thanh) người ta thường dùng những nốt nhạc để ghi những âm có tần số xác định. Tần số dao động càng lớn thì âm càng cao. Khi tăng tần số một âm lên gấp đôi thì ta nói cao độ của âm đó được tăng thêm một quãng tám. Người ta thường chia quãng tám đó thành 12 quãng bằng nhau, mỗi
Quán Ẩm là m ệa án thuật ớp 1, Chênh láh cac độ gi m cá c n múng, , Số cág ản
số của chúng bằng '32 ; với hai âm cách nhau một cung (tức là hai bán cung), tỉ số các tần số của chúng bằng ((75)* = (2 . ở khuông nhạc dưới đây có ghi các nốt nhạc của một "ảm giai" (quãng tám) cùng khoảng cách cao độ giữa hai âm ứng với hai nốt kể nhau. Ăm la của âm giai đó có tần số 440 Hz (do đó, chẳng hạn âm si kế đó có tần số 440 $/2 Hz).
Trong âm nhạc, ngoài các âm riêng lẻ còn có hợp âm (kết hợp các âm thanh). Nhà toán học Pháp Phu-ri-ê (Fourier) đã chứng minh rằng một hàm số tuần hoàn với chu kì T có thể phân tích thành "tổng" của một hằng số với những hàm số tuần hoàn có đồ thị là những đường
hình sin với chu kì (i là số nguyên dương). Điều
đó giúp ta hiểu sâu hơn về hợp âm, hòà âm, âm bội và âm sắc.00:26/-strong/-heart:>:o:-((:-hXem trước khi gửiThả Files vào đây để xem lại trước khi gửi
